题目内容
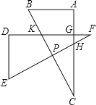
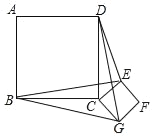
【题目】两个完全相同的矩形纸片![]() 、
、![]() 如图放置,重叠部分是四边形
如图放置,重叠部分是四边形![]() .
.

![]() 试证明四边形
试证明四边形![]() 为菱形;
为菱形;
![]() 与
与![]() 是什么位置关系,试证明.
是什么位置关系,试证明.
【答案】(1)见解析;(2)![]() 垂直平分
垂直平分![]() ,理由见解析
,理由见解析
【解析】
(1)易证四边形BNDM是平行四边形;根据AB=BA′,运用AAS可证明Rt△ABM≌Rt△A′BN,得BM=BN.根据有一邻边相等的平行四边形是菱形得证;
(2)通过Rt△BA′N≌Rt△CDN,得到A′N=CN,推出∠A′NG=∠CNG,根据等腰三角形的性质结论得到结论.
(1)∵两个完全相同的矩形纸片ABCD、BA′DE,根据矩形的对边平行,∴BC∥AD,BE∥DA′,∴四边形BNDM是平行四边形.
∵∠ABM+∠MBN=90°,∠MBN+∠A′BN=90°,∴∠ABM=∠A′BN.
在△ABM和△A′BN中,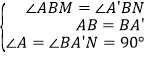 ,∴△ABM≌△A′BN,(ASA),∴BM=BN,∴四边形BNDM是菱形;
,∴△ABM≌△A′BN,(ASA),∴BM=BN,∴四边形BNDM是菱形;
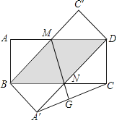
(2)MN垂直平分A′C.理由如下:
在Rt△BA′N与Rt△CDN中,∵![]() ,∴Rt△BA′N≌Rt△CDN,∴A′N=CN.
,∴Rt△BA′N≌Rt△CDN,∴A′N=CN.
∵∠BNM=∠DNM,∠A′NG=∠DNM,∠CNG=∠BNM,∴∠A′NG=∠CNG,∴MN垂直平分A′C.

练习册系列答案
相关题目