��Ŀ����
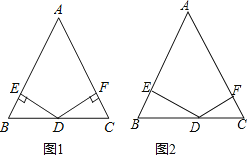
����Ŀ����ͼ1����Rt��ABC�У���ABC=90�㣬BA=BC��ֱ��MN�ǹ���A��ֱ��CD��MN�ڵ�D������BD��
��1���۲��������ʦ�ڿ�����������⣺�߶�DC��AD��BD֮����ʲô������ϵ�������۲�˼����С����һ��˼·����ͼ1������B��BE��BD����MN�ڵ�E�������ó���DC+AD=����BD��
��2��̽��֤��
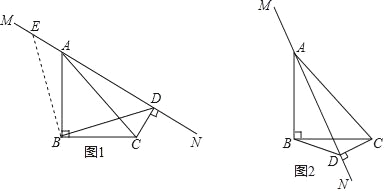
��ֱ��MN�Ƶ�A˳ʱ����ת��ͼ2��λ��д����ʱ�߶�DC��AD��BD֮���������ϵ����֤��
��3����չ����
��ֱ��MN�Ƶ�A��ת�Ĺ����У�����ABD���ȡ�����ֵʱ����CD��Ϊ1����ֱ��дBD�ij���
���𰸡���1��![]() ����2��AD��DC=
����2��AD��DC=![]() BD����3��BD=AD=
BD����3��BD=AD=![]() +1��
+1��
��������
��1������ȫ�������ε��������DC��AD��BD֮���������ϵ
��2������B��BE��BD����MN�ڵ�E��AD��BC��O��
֤��![]() ���õ�
���õ�![]() ��
��![]() ��
��
����![]() Ϊ����ֱ�������Σ��õ�
Ϊ����ֱ�������Σ��õ�![]() ��
��
�ٸ���![]() �����ɽ����.
�����ɽ����.
��3������A��B��C��D�ĵ㹲Բ���õ�����D���߶�AB�Ĵ�ֱƽ����������AB���Ҳ�ʱ����ABD��������
��DA�Ͻ�ȡһ��H��ʹ��CD=DH=1������֤![]() ��
��
��![]() ���ɵó���.
���ɵó���.
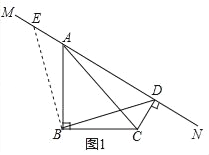
�⣺��1����ͼ1�У�
�����⣺![]() ��
��
��AE=CD��BE=BD��
��CD+AD=AD+AE=DE��
��![]() �ǵ���ֱ�������Σ�
�ǵ���ֱ�������Σ�
��DE=![]() BD��
BD��
��DC+AD=![]() BD��
BD��
�ʴ�Ϊ![]() ��
��
��2��![]() ��
��
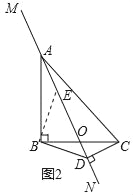
֤������ͼ������B��BE��BD����MN�ڵ�E��AD��BC��O��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ���֡�
���֡�![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() Ϊ����ֱ�������Σ�
Ϊ����ֱ�������Σ�![]() ��
��
��![]() ��
��
��![]() ��
��
��3����ͼ3�У���֪A��B��C��D�ĵ㹲Բ������D���߶�AB�Ĵ�ֱƽ����������AB���Ҳ�ʱ����ABD��������
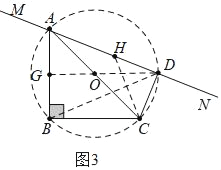
��ʱDG��AB��DB=DA����DA�Ͻ�ȡһ��H��ʹ��CD=DH=1������֤![]() ��
��
��![]() ��
��

����Ŀ��ij��˾ʵ���깤���ƣ�ְ�����깤���ɻ������ʡ�ס��������ҽ�Ʒ�������ɣ�����涨���£�
��Ŀ | ��һ��Ĺ��ʣ���Ԫ�� | һ���ļ��㷽�� |
�������� | 1 | ÿ�����������ͬ |
ס������ | 0.04 | ÿ������0.04 |
ҽ�Ʒ� | 0.1384 | �̶����� |
��1�����������ÿ��������Ϊx���ú�x�Ĵ���ʽ��ʾ������Ļ�������Ϊ ��Ԫ��
��2��ij���ڹ�˾������3�꣬������һ����3���õ���ס��������ҽ�Ʒ���������3����������ܶ��18 %���ʻ�������ÿ����������Ƕ��٣�