题目内容
【题目】巳知二次函数y=x2﹣2x﹣3.
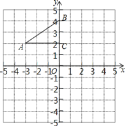
(1)在如图所示平面直角坐标系中画出该函数的图象;
(2)写岀函数值y随x变化的増减情况;
(3)将抛物线怎样平移才能使它经过坐标原点.并写出平移后的函数解析式.(写出一种方式即可)
【答案】(1)图象如图所示;见解析;(2)当x<1时,y随x的增大而减小;当x≥1时,y随x的增大而增大;(3)y=x2﹣4x(或y=(x﹣2)2﹣4).
【解析】
(1)根据题意画出二次函数的图象即可;
(2)根据二次函数的性质即可得到结论;
(3)把二次函数的解析式配方后化为顶点形式,然后把抛物线图象向左平移一个单位,根据平移规律“左加右减”得到平移后的解析式,此时抛物线的图象过原点.
(1)二次函数y=x2﹣2x﹣3的图象如图所示;
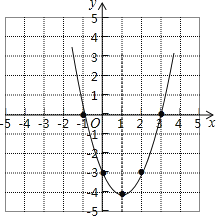
(2)∵二次函数y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴对称轴为x=1,
∴当x<1时,y随x的增大而减小;当x≥1时,y随x的增大而增大;
(3)方法1:向右平移一个单位,平移后的解析式为y=x2﹣4x(或y=(x﹣2)2﹣4),
方法2:向左平移三个单位,平移后的解析式为y=x2+4x(或y=(x+2)2﹣4),
方法3:先向左平移一个单位,再向上平移4个单位或先向上平移4个单位,再左平移1个单位,平移后的解析式为y=x2.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
【题目】抛物线![]() 上部分点的横坐标
上部分点的横坐标![]() ,纵坐标
,纵坐标![]() 的对应值如下表:
的对应值如下表:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
小聪观察上表,得出下面结论:①抛物线与x轴的一个交点为(3,0); ②函数![]() 的最大值为6;③抛物线的对称轴是
的最大值为6;③抛物线的对称轴是![]() ;④在对称轴左侧,y随x增大而增大.其中正确有( )
;④在对称轴左侧,y随x增大而增大.其中正确有( )
A. ①② B. ①③ C. ①②③ D. ①③④