Question

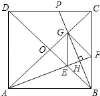
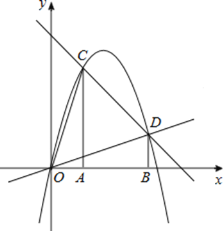
【题目】如图，过、作x轴的垂线，分别交直线于C、D两点抛物线经过O、C、D三点．

求抛物线的表达式；

点M为直线OD上的一个动点，过M作x轴的垂线交抛物线于点N，问是否存在这样的点M，使得以A、C、M、N为顶点的四边形为平行四边形？若存在，求此时点M的横坐标；若不存在，请说明理由；

若沿CD方向平移点C在线段CD上，且不与点D重合，在平移的过程中与重叠部分的面积记为S，试求S的最大值．

Answer 1

【答案】（1）；（2）或或；（3）．

【解析】

（1）利用待定系数法求出抛物线的解析式；

（2）由题意，可知MN∥AC，因为以A、C、M、N为顶点的四边形为平行四边形，则有MN=AC=3．设点M的横坐标为x，则求出MN=|x2﹣4x|；解方程|x2﹣4x|=3，求出x的值，即点M横坐标的值；

（3）设水平方向的平移距离为t（0≤t＜2），利用平移性质求出S的表达式：S（t﹣1）2；当t=1时，s有最大值为．

（1）由题意，可得C（1，3），D（3，1）．

∵抛物线过原点，∴设抛物线的解析式为：y=ax2+bx，∴，解得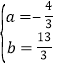，∴抛物线的表达式为：yx2x．

（2）存在．

设直线OD解析式为y=kx，将D（3，1）代入，求得k，∴直线OD解析式为yx．

设点M的横坐标为x，则M（x，x），N（x，x2x），∴MN=|yM﹣yN|=|x﹣（x2x）|=|x2﹣4x|．

由题意，可知MN∥AC，因为以A、C、M、N为顶点的四边形为平行四边形，则有MN=AC=3，∴|x2﹣4x|=3．

若x2﹣4x=3，整理得：4x2﹣12x﹣9=0，解得：x或x；

若x2﹣4x=﹣3，整理得：4x2﹣12x+9=0，解得：x，∴存在满足条件的点M，点M的横坐标为：或或．

（3）∵C（1，3），D（3，1），∴易得直线OC的解析式为y=3x，直线OD的解析式为yx．

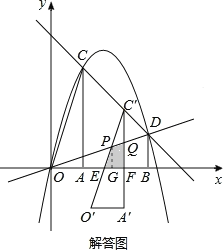
如解答图所示，设平移中的三角形为△A'O'C'，点C'在线段CD上．

设O'C'与x轴交于点E，与直线OD交于点P；

设A'C'与x轴交于点F，与直线OD交于点Q．

设水平方向的平移距离为t（0≤t＜2），则图中AF=t，F（1+t，0），Q（1+t，t），C'（1+t，3﹣t）．

设直线O'C'的解析式为y=3x+b，将C'（1+t，3﹣t）代入得：b=﹣4t，∴直线O'C'的解析式为y=3x﹣4t，∴E（t，0）．

联立y=3x﹣4t与yx，解得：xt，∴P（t，t）．

过点P作PG⊥x轴于点G，则PGt，∴S=S△OFQ﹣S△OEPOFFQOEPG

（1+t）（t）tt

（t﹣1）2

当t=1时，S有最大值为，∴S的最大值为．