题目内容
【题目】已知⊙O中,AC为直径,MA、MB分别切⊙O于点A、B.

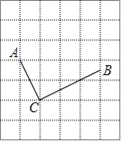
(1)如图①,若∠BAC=23°,求∠AMB的大小;
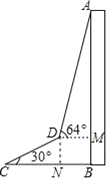
(Ⅱ)如图②,过点B作BD∥MA,交AC于点E,交⊙O于点D,若BD=MA,求∠AMB的大小.
【答案】(1)∠AMB=46°;(Ⅱ)∠AMB=60°.
【解析】试题分析:(1)根据切线性质求出∠OBM=∠OAM=90°,根据圆周角定理求出∠COB,求出∠BOA,即可求出答案;
(2)连接AB、AD,得出平行四边形,推出MB=AD,推出AB=AD,求出等边三角形AMB,即可得出答案.
解:(1)连接OB,
∵MA、MB分别切⊙O于A、B,
∴∠OBM=∠OAM=90°,
∵弧BC对的圆周角是∠BAC,圆心角是∠BOC,∠BAC=23°,
∴∠BOC=2∠BAC=46°,
∴∠BOA=180°﹣46°=134°,
∴∠AMB=360°﹣90°﹣90°﹣134°=46°.

(2)连接AD,AB,
∵BD∥AM,DB=AM,
∴四边形BMAD是平行四边形,
∴BM=AD,
∵MA切⊙O于A,
∴AC⊥AM,
∵BD∥AM,
∴BD⊥AC,
∵AC过O,
∴BE=DE,
∴AB=AD=BM,
∵MA、MB分别切⊙O于A、B,
∴MA=MB,
∴BM=MA=AB,
∴△BMA是等边三角形,
∴∠AMB=60°.

 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案【题目】小林在某商店购买商品A、B共三次,只有一次购买时,商品A、B同时打折(折扣相同),其余两次均按标价购买.三次购买商品A、B的数量和费用如下表:
购买商品A的数量/个 | 购买商品B的数量/个 | 购买总费用/元 | |
第一次购物 | 6 | 5 | 1140 |
第二次购物 | 3 | 7 | 1110 |
第三次购物 | 9 | 8 | 1062 |
(1)小林以折扣价购买商品A、B是第 次购物;
(2)求出商品A、B的标价;
(3)若商品A、B的折扣相同,问商店是打几折出售这两种商品的?