题目内容
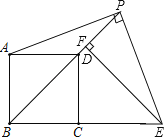
【题目】如图,点M是矩形ABCD的边AD延长线上一点,以AM为直径的⊙O交矩形对角线AC于点F,在线段CD上取一点E,连接EF,使EC=EF.

(1)求证:EF是⊙O的切线;
(2)若cos∠CAD=![]() ,AF=6,MD=2,求FC的长.
,AF=6,MD=2,求FC的长.
【答案】(1)见解析;(2)FC=![]() .
.
【解析】
(1)根据等腰三角形的性质和直角三角形两锐角互余证得∠EFC+∠OFA=90°,即可证得∠EFO=90°,即EF⊥OF,从而证得结论;
(2)根据圆周角定理得出∠AFM=90°,通过解直角三角形求得AM=10,得出AD=8,进而求得![]() ,即可求得
,即可求得![]() .
.
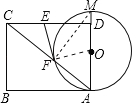
(1)证明:连接OF,
∵四边形ABCD是矩形,
∴∠ADC=90°,
∴∠CAD+∠DCA=90°,
∵EC=EF,
∴∠DCA=∠EFC,
∵OA=OF,
∴∠CAD=∠OFA,
∴∠EFC+∠OFA=90°,
∴∠EFO=90°,
∴EF⊥OF,
∵OF是半径,
∴EF是⊙O的切线;
(2)连接MF,
∵AM是直径,
∴∠AFM=90°,
在Rt△AFM中,![]() ,
,
∵AF=6,
∴![]() ,
,
∴AM=10,
∵MD=2,
∴AD=8,
在Rt△ADC中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
相关题目
【题目】已知二次函数![]() .
.
![]() 该函数图象的对称轴是________,顶点坐标________;
该函数图象的对称轴是________,顶点坐标________;
![]() 选取适当的数据填入下表,并描点画出函数图象;
选取适当的数据填入下表,并描点画出函数图象;
| … | … | |||||
| … | … |
![]() 求抛物线与坐标轴的交点坐标;
求抛物线与坐标轴的交点坐标;
![]() 利用图象直接回答当
利用图象直接回答当![]() 为何值时,函数值
为何值时,函数值![]() 大于
大于![]() ?
?