题目内容
如图所示,已知直线y=
x与抛物线y=ax2+b(a≠0)交于A(-4,-2),B(6,3)两点.抛物线与y轴的交点为C.
(1)求这个抛物线的解析式;
(2)在抛物线上存在点M,是△MAB是以AB为底边的等腰三角形,求点M的坐标;
(3)在抛物线上是否存在点P使得△PAC的面积是△ABC面积的
?若存在,试求出此时点P 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
| 1 |
| 2 |
(1)求这个抛物线的解析式;
(2)在抛物线上存在点M,是△MAB是以AB为底边的等腰三角形,求点M的坐标;
(3)在抛物线上是否存在点P使得△PAC的面积是△ABC面积的
| 3 |
| 4 |
 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.(1)由题意,得:
,
解得
;
∴抛物线的解析式为y=
x2-6;
(2)如图1,取AB的中点E,则E(1,
);过E作直线l垂直于AB;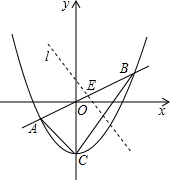
∵直线AB的解析式为:y=
x,∴可设直线l的解析式为y=-2x+b;
∵直线l过E(1,
),则有:
=-2+b,b=
;
∴直线l的解析式为:y=-2x+
;联立抛物线的解析式有:
,
解得
,
∴M(-4+5
,
-10
)或(-4-5
,
+10
);
(3)过B作BF⊥AC于F,交x轴于N;
过F作FH⊥y轴于H,过A作AG⊥y轴于G;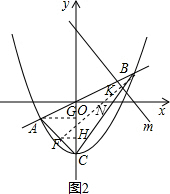
在BF上截取BK=
BF;
∵A(-4,-2),B(6,3),C(0,-6)
∴S△ABC=
OC×|xB-xA|
=
×6×10=30;
Rt△AGC中,AG=CG=4,则∠GAC=∠HFC=45°,AC=4
;
∵∠BFC=90°,
∴∠BNx=∠BFH=90°-45°=45°;
易知BN=3
,BK=
BF=
×
=
×
=
;
∴NK=BN-BK=
;
由于∠BNx=45°,可求得K(
,
);
易知直线AC的解析式为:y=-x-6,过K作直线m平行于AC,可设直线m的解析式为:y=-x+h,则:
-
+h=
,h=
;
∴直线m的解析式为y=-x+
;
由于△ABC与△PAC等底不等高,
则面积比等于高的比,由于KF=
BF,那么P点必为直线m与抛物线的交点,联立直线m与抛物线的解析式可得:
,
解得
,
;
∴P点的坐标为(5,
)或(-9,
).
|
解得
|
∴抛物线的解析式为y=
| 1 |
| 4 |
(2)如图1,取AB的中点E,则E(1,
| 1 |
| 2 |

∵直线AB的解析式为:y=
| 1 |
| 2 |
∵直线l过E(1,
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
∴直线l的解析式为:y=-2x+
| 5 |
| 2 |
|
解得
|
|
∴M(-4+5
| 2 |
| 21 |
| 2 |
| 2 |
| 2 |
| 21 |
| 2 |
| 2 |
(3)过B作BF⊥AC于F,交x轴于N;
过F作FH⊥y轴于H,过A作AG⊥y轴于G;

在BF上截取BK=
| 1 |
| 4 |
∵A(-4,-2),B(6,3),C(0,-6)
∴S△ABC=
| 1 |
| 2 |
=
| 1 |
| 2 |
Rt△AGC中,AG=CG=4,则∠GAC=∠HFC=45°,AC=4
| 2 |
∵∠BFC=90°,
∴∠BNx=∠BFH=90°-45°=45°;
易知BN=3
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 2S△ABC |
| AC |
| 1 |
| 4 |
| 2×30 | ||
4
|
15
| ||
| 8 |
∴NK=BN-BK=
9
| ||
| 8 |
由于∠BNx=45°,可求得K(
| 33 |
| 8 |
| 9 |
| 8 |
易知直线AC的解析式为:y=-x-6,过K作直线m平行于AC,可设直线m的解析式为:y=-x+h,则:
-
| 33 |
| 8 |
| 9 |
| 8 |
| 21 |
| 4 |
∴直线m的解析式为y=-x+
| 21 |
| 4 |
由于△ABC与△PAC等底不等高,
则面积比等于高的比,由于KF=
| 3 |
| 4 |
|
解得
|
|
∴P点的坐标为(5,
| 1 |
| 4 |
| 57 |
| 4 |

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目





 在x轴上,过A、B、C三点的抛物线表达式为
在x轴上,过A、B、C三点的抛物线表达式为