题目内容
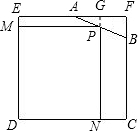
如图所示,在边长为4的正方形EFCD上截去一角,成为五边形ABCDE,其中AF=2,BF=1,在AB上取一点P,设P到DE的距离PM=x,P到CD的距离PN=y,试写出矩形PMDN的面积S与x之间的函数关系式.


∵在边长为4的正方形EFCD上截去一角,成为五边形ABCDE,
∴存在线段AB且AB的位置已经固定,
当P和B重合时,x=4,即x≤4
当x=2,P和A重合,即x≥2,
∴x的取值范围是2≤x≤4,
如图,S矩形PNDM=xy,且2≤x≤4,
延长NP交EF于G,显然PG∥BF,
∴△AGP∽△AFB,
∴
=
,
即
=
,
∴y=-
x+5,
∴S=xy=-
x2+5x,
即S=-
x2+5x(2≤x≤4).
∴存在线段AB且AB的位置已经固定,
当P和B重合时,x=4,即x≤4
当x=2,P和A重合,即x≥2,
∴x的取值范围是2≤x≤4,
如图,S矩形PNDM=xy,且2≤x≤4,
延长NP交EF于G,显然PG∥BF,
∴△AGP∽△AFB,
∴
| PG |
| BF |
| AG |
| AF |
即
| 4-y |
| 1 |
| x-2 |
| 2 |
∴y=-
| 1 |
| 2 |
∴S=xy=-
| 1 |
| 2 |
即S=-
| 1 |
| 2 |


练习册系列答案
相关题目


 线y=-
线y=-
 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. 单位长度的速度从点A出发,沿A?B运动,连接PQ,CB,设点P的运动时间t秒.(0<t<2).
单位长度的速度从点A出发,沿A?B运动,连接PQ,CB,设点P的运动时间t秒.(0<t<2).