题目内容
已知关于x的一元二次方程
x2+(m-2)x+2m-6=0.
(1)求证:无论m取任何实数,方程都有两个实数根;
(2)当m<3时,关于x的二次函数y=
x2+(m-2)x+2m-6的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,且2AB=3OC,求m的值;
(3)在(2)的条件下,过点C作直线l∥x轴,将二次函数图象在y轴左侧的部分沿直线l翻折,二次函数图象的其余部分保持不变,得到一个新的图象,记为G.请你结合图象回答:当直线y=
x+b与图象G只有一个公共点时,b的取值范围.

| 1 |
| 2 |
(1)求证:无论m取任何实数,方程都有两个实数根;
(2)当m<3时,关于x的二次函数y=
| 1 |
| 2 |
(3)在(2)的条件下,过点C作直线l∥x轴,将二次函数图象在y轴左侧的部分沿直线l翻折,二次函数图象的其余部分保持不变,得到一个新的图象,记为G.请你结合图象回答:当直线y=
| 1 |
| 3 |

(1)根据题意,得
△=(m-2)2-4×
×(2m-6)
=(m-4)2,
∵无论m为任何数时,都有(m-4)2≥0,即△≥0.
∴无论m取任何实数,方程都有两个实数根;
(2)由题意,得
当y=0时,则
x2+(m-2)x+2m-6=0,
解得:x1=6-2m,x2=-2,
∵m<3,点A在点B的左侧,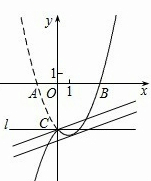
∴A(-2,0),B(-2m+6,0),
∴OA=2,OB=-2m+6.
当x=0时,y=2m-6,
∴C(0,2m-6),
∴OC=-(2m-6)=-2m+6.
∵2AB=3OC,
∴2(2-2m+6)=3(-2m+6),
解得:m=1;
(3)如图,当m=1时,抛物线的解析式为y=
x2-x-4,
点C的坐标为(0,-4).
当直线y=
x+b经过点C时,可得b=-4,
当直线y=
x+b(b<-4)与函数y=
x2-x-4(x>0)的图象只有一个公共点时,得
x+b═
x2-x-4.
整理得:3x2-8x-6b-24=0,
∴△=(-8)2-4×3×(-6b-24)=0,
解得:b=-
.
结合图象可知,符合题意的b的取值范围为b>-4或b<-
.
△=(m-2)2-4×
| 1 |
| 2 |
=(m-4)2,
∵无论m为任何数时,都有(m-4)2≥0,即△≥0.
∴无论m取任何实数,方程都有两个实数根;
(2)由题意,得
当y=0时,则
| 1 |
| 2 |
解得:x1=6-2m,x2=-2,
∵m<3,点A在点B的左侧,

∴A(-2,0),B(-2m+6,0),
∴OA=2,OB=-2m+6.
当x=0时,y=2m-6,
∴C(0,2m-6),
∴OC=-(2m-6)=-2m+6.
∵2AB=3OC,
∴2(2-2m+6)=3(-2m+6),
解得:m=1;
(3)如图,当m=1时,抛物线的解析式为y=
| 1 |
| 2 |
点C的坐标为(0,-4).
当直线y=
| 1 |
| 3 |
当直线y=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
整理得:3x2-8x-6b-24=0,
∴△=(-8)2-4×3×(-6b-24)=0,
解得:b=-
| 44 |
| 9 |
结合图象可知,符合题意的b的取值范围为b>-4或b<-
| 44 |
| 9 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 线y=-
线y=- 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. )两点,设OA•OB=3(O为坐标系原点).
)两点,设OA•OB=3(O为坐标系原点).