题目内容
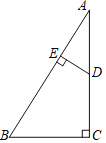
【题目】如图，菱形ABCD的对角线AC，BD相交于点O，且DE∥AC，AE∥BD．求证：四边形AODE是矩形．
【答案】证明：∵四边形ABCD为菱形，
∴AC⊥BD，
∴∠AOD=90°，
∵DE∥AC，AE∥BD，
∴四边形AODE为平行四边形，
∴四边形AODE是矩形．
【解析】先由两组平行可得出四边形AODE为平行四边形，再由菱形的性质对角线互相垂直证出结论.
【考点精析】根据题目的已知条件，利用菱形的性质和矩形的判定方法的相关知识可以得到问题的答案，需要掌握菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半；有一个角是直角的平行四边形叫做矩形；有三个角是直角的四边形是矩形；两条对角线相等的平行四边形是矩形．
练习册系列答案
快乐小博士巩固与提高系列答案
相关题目
【题目】为响应国家节能减排的号召，鼓励居民节约用电，各省市先后出台了居民用电“阶梯价格”制度，下表是某市的电价标准（每月）．
阶梯 | 一户居民每月用电量x（单位：度） | 电费价格（单位：元/度） |
一档 | 0＜x≤180 | a |
二档 | 180＜x≤280 | b |
三档 | x＞280 | 0.82 |
（1）已知小华家四月份用电200度，缴纳电费105元；五月份用电230度，缴纳电费122.1元，请你根据以上数据，求出表格中a，b的值；
（2）六月份是用电高峰期，小华家计划六月份电费支出不超过208元，那么小华家六月份最多可用电多少度？
