题目内容
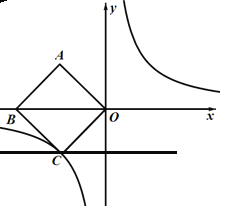
【题目】如图，在平面直角坐标系
中，正方形ABCO的对角线BO在x 轴上，若正方形ABCO的边长为
，点B在x负半轴上，反比例函数
的图象经过C点．
（1）求该反比例函数的解析式；
（2）当函数值
＞-2时，请直接写出自变量x的取值范围；
（3）若点P是反比例函数上的一点，且△PBO的面积恰好等于正方形ABCO的面积，求点P的坐标．
【答案】（1）
；（2）x＜-2或x＞0 （3）（1，4）或（﹣1，﹣4）．
【解析】分析：(1)利用正方形边长和正方形位置特点，可求得C点坐标，待定系数法求反比例函数解析式.(2)利用反比例函数与不等式的关系，数形结合求不等式.(3)利用面积相等，列方程，求解P点坐标.
详解：(1)AO=
,根据勾股定理知，BO=4,所以C(-2,-2), 反比例函数
的图象经过C点，
所以
=-2,k=4. 
.
(2)画出y=-2,数形结合知，x＜-2或x＞0
（3）设P(x, 
,所以S△PBO=SABCO,
=AO2,
,x=
,
所以P（1，4）或（﹣1，﹣4）．
练习册系列答案
相关题目
