题目内容
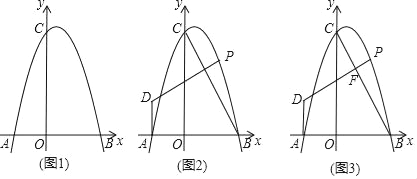
【题目】已知:如图,抛物线y=ax2+bx+6交x轴于A(﹣2,0),B(3,0)两点,交y轴于点C.
(1)求a,b的值;
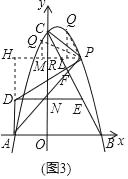
(2)连接BC,点P为第一象限抛物线上一点,过点A作AD⊥x轴,过点P作PD⊥BC于交直线AD于点D,设点P的横坐标为t,AD长为d,求d与t的函数关系式(请求出自变量t的取值范围);
(3)在(2)的条件下,DP与BC交于点F,过点D作DE∥AB交BC于点E,点Q为直线DP上方抛物线上一点,连接AP、PC,若DP=CE,∠QPC=∠APD时,求点Q坐标.
【答案】(1)a=-1,b=1;(2)d=﹣t2+![]() t+5(0<t<3);(3)点Q坐标为Q(1,6)或Q(﹣
t+5(0<t<3);(3)点Q坐标为Q(1,6)或Q(﹣![]() ,
, ![]() ).
).
【解析】试题分析:
(1)把A、B两点的坐标代入抛物线的解析式列出关于a、b的二元一次方程组,解方程组即可求得a、b的值;
(2)如下图2、过点P作PG⊥DE于点K,交x轴于点G,作DK⊥PG于点K,则由已知条件易得∠BCO=∠PDK,由此可得tan∠PDK=![]() =tan∠BCO,结合OB=3,OC=6,DK=t+2可得PK=
=tan∠BCO,结合OB=3,OC=6,DK=t+2可得PK=![]() DK=
DK=![]() (t+2);再证四边形ADKG是矩形可得KG=AD=d=PG-PK结合PG=-t2+t+6即可得到d与t间的函数关系式了,由点P在第一象限的图象上可得0<t<3;
(t+2);再证四边形ADKG是矩形可得KG=AD=d=PG-PK结合PG=-t2+t+6即可得到d与t间的函数关系式了,由点P在第一象限的图象上可得0<t<3;
(3)如下图3,过点P作PH⊥AD于点H交y轴于点R,由已知条件易证△PHD≌△CNE,从而可得PH=CN,结合CN=OC-ON,PH=t+2可得关于t的方程t+2=t2﹣![]() t+1,解方程可得t1=2,t2=﹣
t+1,解方程可得t1=2,t2=﹣![]() (舍),把t=2代入抛物线y=﹣x2+x+6=4,可得点P(2,4),由此可得PR=CR,PH=AH,从而可得∠APC=90°结合∠QPC=∠APD可得∠QPD=90°,然后分点P在第一象限的抛物线上和第三象限的抛物线上两种情况讨论计算即可得到对应的点Q的坐标.
(舍),把t=2代入抛物线y=﹣x2+x+6=4,可得点P(2,4),由此可得PR=CR,PH=AH,从而可得∠APC=90°结合∠QPC=∠APD可得∠QPD=90°,然后分点P在第一象限的抛物线上和第三象限的抛物线上两种情况讨论计算即可得到对应的点Q的坐标.
试题解析:
(1)∵抛物线y=ax2+bx+6过点A(﹣2,0),B(3,0),则
![]() ,解得:
,解得: ![]() ,
,
故抛物线解析式为y=﹣x2+x+6;
(2)如下图2,过点P作PG⊥x于点G,过点D作DK∥x轴交PG于点K,
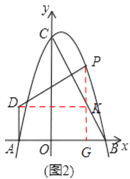
∵PD⊥BC,DE⊥y轴,∠BCO=∠PDK,OB=3,OC=6
∴tan∠BCO=tan∠PDK=![]() ,DK=t+2,PK=
,DK=t+2,PK=![]() DK=
DK=![]() (t+2),
(t+2),
∵DK∥AB,AD⊥AB,
∴四边形ADKG为矩形,
∴AD=KG,
d=AD=KG=PG﹣PK=﹣t2+t+6﹣![]() (t+2)=﹣t2+
(t+2)=﹣t2+![]() t+5(0<t<3);
t+5(0<t<3);
(3)如图3,过点P作PH⊥AD于点H,
在△PHD与△CNE中, 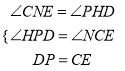 ,
,
∴△PHD≌△CNE,
∴PH=CN=OC﹣ON,
∵四边形ADON为矩形,
∴CN=6﹣(﹣t2+![]() t+5)=t2﹣
t+5)=t2﹣![]() t+1,PH=t+2,
t+1,PH=t+2,
∴t+2=t2﹣![]() t+1,
t+1,
解得t1=2,t2=﹣![]() (舍),
(舍),
把t=2代入抛物线y=﹣x2+x+6=4,
∴点P(2,4),
∵PH与y轴交于点R,PR=CR=2,
∴∠CPR=45°,PH=AH=4,
∴∠APH=45°,
∴∠APC=90°,
∵∠QPC=∠APD,
∴∠QPD=90°,
当点Q在第一象限时,过点Q作QL⊥PH于点L,
∴∠LQP=∠HPD,
∴tan∠LQP=tan∠HPD=![]() ,
,
设点Q(m,﹣m2+m+6),则PL=2﹣m,QL=﹣m2+m+2,则
![]() =
=![]() ,
,
解得m1=1,m2=2(舍),
把m=1 代入﹣m2+m+6=6,
∴Q(1,6),
当点Q在第二象限时,过点Q作QM⊥PH,
∵∠CPH=∠APH=45°∠QPC=∠APD,
∴∠QPM=∠DPH tan∠QPM=tan∠DPH=![]() ,
,
设点Q(n,﹣n2+n+6)PM=2﹣n QM=﹣n2+n+2,
∴![]() =
=![]() ,
,
解得n1=﹣![]() ,n2=2(舍),
,n2=2(舍),
把n=1﹣![]() 代入﹣n2+n+6=
代入﹣n2+n+6=![]() ,
,
∴Q(﹣![]() ,
, ![]() ).
).
综上所述,点Q坐标为Q(1,6)或Q(﹣![]() ,
, ![]() ).
).