题目内容
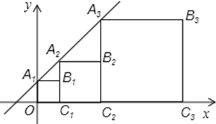
【题目】正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2),则B5的坐标是_____________ 。
【答案】(31,16)
【解析】
首先由B1的坐标为(1,1),点B2的坐标为(3,2),可得正方形A1B1C1O1边长为1,正方形A2B2C2C1边长为2,即可求得A1的坐标是(0,1),A2的坐标是:(1,2),然后又待定系数法求得直线A1A2的解析式,由解析式即可求得点A3的坐标,继而可得点B3的坐标,观察可得规律Bn的坐标是(2n-1,2n-1).
∵B1的坐标为(1,1),点B2的坐标为(3,2)
∴正方形A1B1C1O1边长为1,正方形A2B2C2C1边长为2
∴A1的坐标是(0,1),A2的坐标是:(1,2)
设直线A1A2的解析式为:y=kx+b
∴![]()
解得:![]()
∴直线A1A2的解析式是:y=x+1
∵点B2的坐标为(3,2)
∴点A3的坐标为(3,4)
∴点B3的坐标为(7,4)
∴Bn的横坐标是:2n-1,纵坐标是:2n1
∴Bn的坐标是(2n1,2n1)
故点B5的坐标为(31,16).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目