Question

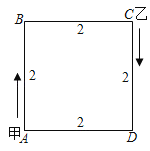
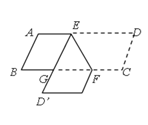
【题目】如图，在□ABCD中，点E，F分别在边AD、BC上，EF=2，∠DEF=60°将四边形EFCD沿EF翻折，得到四边形EFC’D’，ED’交BC于点G，则△GEF的周长为________．

Answer 1

【答案】6；

【解析】分析：根据平行四边形的性质得到AD∥BC，由平行线的性质得到∠AEG=∠EGF，根据折叠的性质得到∠GEF=∠DEF=60°，推出△EGF是等边三角形，于是得到结论．

详解：∵四边形ABCD是平行四边形，

∴AD∥BC，

∴∠AEG=∠EGF，

∵将四边形EFCD沿EF翻折，得到EFC′D′，

∴∠GEF=∠DEF=60°，

∴∠AEG=60°，

∴∠EGF=60°，

∴△EGF是等边三角形，

∵EF=2，

∴△GEF的周长=6，

故答案为6．

题睛：本题考查了翻折变换的性质、平行四边形的性质、等边三角形的判定，熟练掌握翻折变换的性质是解决问题的关键．