题目内容
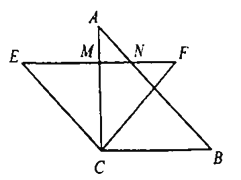
【题目】把两个全等的等腰直角三角形如图放置在一起
，点
关于
对称
交，
于点
，则
与
的面积比为（ ）
A.
B.
C.
D.
【答案】D
【解析】
由轴对称性质得EF⊥AC，由∠A=45°，得出△AMN是等腰直角三角形，由等腰直角三角形的性质得CM=EM=
CE，由△ECF≌△ACB得出AC=CE=BC，则AM=（1-）AC，由等腰直角三角形面积公式即可得出结果．
解：∵△ACB是等腰直角三角形，
∴AC=BC，∠A=45°，
∵点E，F关于AC对称，
∴EF⊥AC，
∵∠A=45°，
∴△AMN是等腰直角三角形，
∵△ECF是等腰直角三角形，
∴CM=EM=
=CE,
∵△ECF≌△ACB，
∴AC=CE=BC，
∴AM=AC-CM=AC-AC=（1-）AC，
∴
=
=
= 
= 
.
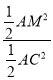故选：D.
练习册系列答案
相关题目
【题目】为了鼓励市民节约用水，某市自来水公司对每户用水量进行了分段计费，每户每月用水量在规定吨数以下的收费标准相同，规定吨数以上的超过部分收费相同．如表是小明家1﹣4月用水量和交费情况：
月份 | 1 | 2 | 3 | 4 |
用水量（吨） | 6 | 8 | 12 | 15 |
费用（元） | 12 | 16 | 28 | 37 |
（Ⅰ）若小明家5月份用水25吨，则应缴多少元水费？
（Ⅱ）若该户居民某月份用水为
吨，则应收水费多少元？（用含的代数式表示，并化简）．
