题目内容
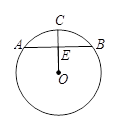
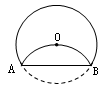
如图,AB是⊙O的弦,OC⊥AB于C,如果AB= 8,OC=3,那么⊙O的半径为____________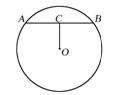

5
考点:
分析:连接OA,因为OC为圆心O到AB的距离,所以OC⊥AB,根据垂径定理,AC=CB=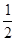 AB=4,因为OC=3,在Rt△AOC中,利用勾股定理,可以求出OA=5.
AB=4,因为OC=3,在Rt△AOC中,利用勾股定理,可以求出OA=5.
解:如图,连接OA,
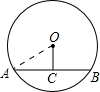
∵OC为圆心O到AB的距离,
∴OC⊥AB,
∵AB=8,
∴AC=CB=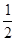 AB=4,
AB=4,
∵圆O的半径为5,
∴OC=3
在Rt△AOC中,根据勾股定理,OA=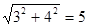 ,故应填5.
,故应填5.
点评:解决与弦有关的问题时,往往需构造以半径、弦心距和弦长的一半为三边的直角三角形,借助勾股定理解决.
分析:连接OA,因为OC为圆心O到AB的距离,所以OC⊥AB,根据垂径定理,AC=CB=
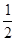 AB=4,因为OC=3,在Rt△AOC中,利用勾股定理,可以求出OA=5.
AB=4,因为OC=3,在Rt△AOC中,利用勾股定理,可以求出OA=5.解:如图,连接OA,

∵OC为圆心O到AB的距离,
∴OC⊥AB,
∵AB=8,
∴AC=CB=
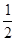 AB=4,
AB=4,∵圆O的半径为5,
∴OC=3
在Rt△AOC中,根据勾股定理,OA=
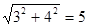 ,故应填5.
,故应填5.点评:解决与弦有关的问题时,往往需构造以半径、弦心距和弦长的一半为三边的直角三角形,借助勾股定理解决.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
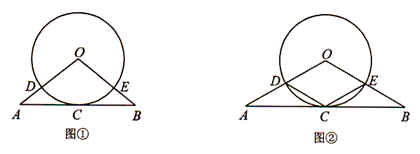
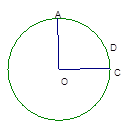
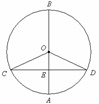
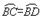
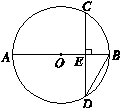
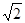 ),且AC⊥
),且AC⊥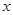 轴,BD⊥
轴,BD⊥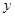 轴.则四边形ABCD的面积为______________.
轴.则四边形ABCD的面积为______________.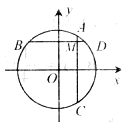
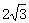 cm
cm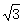 cm
cm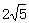 cm[
cm[