题目内容
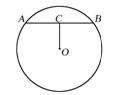
(本小题6分) 如图,OA、OC是⊙O的半径,OA=1,且OC⊥OA,点D在弧AC上,弧AD=2弧CD,在OC求一点P,使PA+PD最小,并求这个最小值.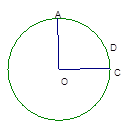

解:延长AO交⊙O于B,联结BD交OC于点P, 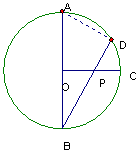
则点P为所求 ------------------------2分
联结AD
∵AB为⊙O的直径
∴∠ADB=90° ------------------------3分
∵OC⊥OA,弧AD=2弧CD
∴∠ABD=30° -------------------------5分
∵OA=1
∴AB=2
∴BD=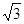
即PA+PD最小值为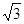

则点P为所求 ------------------------2分
联结AD
∵AB为⊙O的直径
∴∠ADB=90° ------------------------3分
∵OC⊥OA,弧AD=2弧CD
∴∠ABD=30° -------------------------5分
∵OA=1
∴AB=2
∴BD=
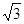
即PA+PD最小值为
略

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目

 与⊙O
与⊙O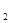 外切,⊙O
外切,⊙O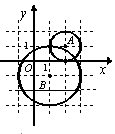
 (4,0)两点,OA=3,点P是y轴上的一个动点,PD切⊙O于点D,则PD的最小值是 .
(4,0)两点,OA=3,点P是y轴上的一个动点,PD切⊙O于点D,则PD的最小值是 .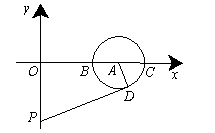
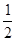 x+4(即直线l2),l2与x轴相交于点A.点P从原点O出发,向x轴的正方向作匀速运动,速度为每秒1个单位,同时点Q从A点出发,向x轴的负方向作匀速运动,速度为每秒2个单位.设运动了t秒.
x+4(即直线l2),l2与x轴相交于点A.点P从原点O出发,向x轴的正方向作匀速运动,速度为每秒1个单位,同时点Q从A点出发,向x轴的负方向作匀速运动,速度为每秒2个单位.设运动了t秒.