题目内容
(本题10分)已知,如图,△OAB中,OA=OB,⊙O经过AB的中点C,且与OA、OB分别交于点D、E.
小题1:(1) 如图①,判断直线AB与⊙O的位置关系并说明理由;
小题2:(2) 如图②,连接CD、CE,当△OAB满足什么条件时,四边形ODCE为菱形,并证明你的结论。
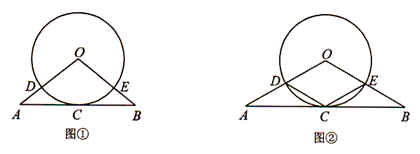
小题1:(1) 如图①,判断直线AB与⊙O的位置关系并说明理由;
小题2:(2) 如图②,连接CD、CE,当△OAB满足什么条件时,四边形ODCE为菱形,并证明你的结论。
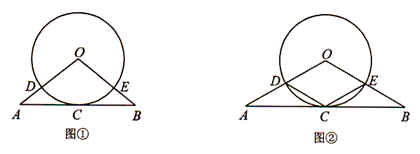
小题1:相切
小题2:2)∠A=30度(或∠B=30度或∠AOB=120度)
分析:
(1)连接OC.利用等腰三角形的“三合一”的性质证得OC⊥AB,即直线AB与⊙O相切;
(2)根据菱形的性质,求得OD=CD,则△ODC为等边三角形,可得出∠A=30°。
解答:
解:(1)相切;
理由如下:如图①,连接OC。
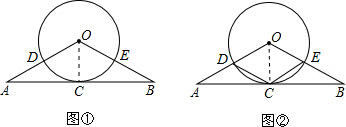
∵OA=OB,点C是线段AB的中点,
∴OC⊥AB;
又∵OC是⊙O的半径,点C在⊙O上,
∴直线AB与⊙O相切。
(2)如图②,连接OC,则OC=OD;
∵四边形ODCE为菱形,
∴OD=CD,
∴OC=OD=CD,
∴△ODC为等边三角形,
∴∠AOC=60°。
由(1)知,∠OCA=90°,
∴∠A=30°(或∠B=30°或∠AOB=120°)。
点评:本题考查了切线的判定与性质、菱形的性质.菱形是四条边都相等的平行四边形。

练习册系列答案
相关题目

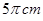 ,它所对的圆心角为
,它所对的圆心角为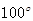 ,则该圆的半径为( )
,则该圆的半径为( )
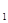 与⊙O
与⊙O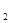 外切,⊙O
外切,⊙O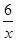 (x>0)图象上的任意一点,以P为圆心,PO为半径的圆与x、y轴分别交于点A、B.
(x>0)图象上的任意一点,以P为圆心,PO为半径的圆与x、y轴分别交于点A、B.