题目内容
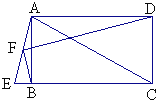
【题目】如图，将
绕点B顺时针旋转
，得到
，连接
、
.
(1)求证：
为等边三角形；
(2)若
，
，
，求
；
(3)已知
，点
在四边形
内部（包括边界）.若点F由点B运动至点E,其运动过程满足
，求点运动路径的长.
【答案】（1）见解析；（2）
；（3）l
=
.
【解析】
（1）由旋转的性质可得结论；
（2）根据等边三角形和勾股定理得
，得
，
可得
从而可求出；
（3）将
绕点
逆时针旋转
，得到
，连结
.证得
是等边三角形，进而证明
，求出
.从而可求出
的长.
（1）由旋转的性质得：
,
∵
,
∴
为等边三角形；
（2）∵为等边三角形，
∴
.
由旋转得：
,
,
.
∵
,
,
,
∴
,
∴,
∴,
∴,
∴,
∴；
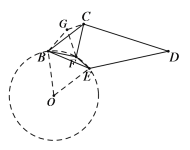
（3）如图，将△BEF绕点逆时针旋转，得到，连结.
∵
，
，
∴是等边三角形，
∴
，
.
∵
,
∴
,
∴，
∴
，
∴.
∵动点
在四边形
内部运动，且满足
，
因此以
为边向外作等边三角形
，则点运动路径劣弧,
∴l=.
练习册系列答案
阅读快车系列答案
相关题目
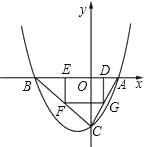
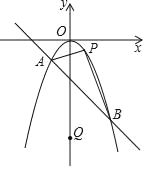
【题目】如图，已知抛物线P：y=ax2+bx+c（a≠0）与x轴交于A、B两点（点A在x轴的正半轴上），与y轴交于点C，矩形DEFG的一条边DE在线段AB上，顶点F、G分别在线段BC、AC上，抛物线P上部分点的横坐标对应的纵坐标如下：
x | … | ﹣3 | ﹣2 | 1 | 2 | … |
y | … |
| ﹣4 |
| 0 | … |
（1）求A、B、C三点的坐标；
（2）若点D的坐标为（m，0），矩形DEFG的面积为S，求S与m的函数关系，并指出m的取值范围；
（3）当矩形DEFG的面积S取最大值时，连接DF并延长至点M，使FM=kDF，若点M不在抛物线P上，求k的取值范围．
