题目内容
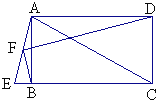
【题目】如图所示，矩形ABCD中，点E在CB的延长线上，使CE＝AC，连接AE，点F是AE的中点，连接BF、DF，求证：BF⊥DF．
【答案】见解析.
【解析】
延长BF，交DA的延长线于点M，连接BD，进而求证△AFM≌△EFB，得AM=BE，FB=FM，即可求得BC+BE=AD+AM，进而求得BD=BM，根据等腰三角形三线合一的性质即可求证BF⊥DF．
延长BF，交DA的延长线于点M，连接BD．
∵四边形ABCD是矩形，∴MD∥BC，∴∠AMF=∠EBF，∠E=∠MAF，又FA=FE，∴△AFM≌△EFB，∴AM=BE，FB=FM．
∵矩形ABCD中，∴AC=BD，AD=BC，∴BC+BE=AD+AM，即CE=MD．
∵CE=AC，∴AC=CE= BD =DM．
∵FB=FM，∴BF⊥DF．
练习册系列答案
步步高口算题卡系列答案
点睛新教材全能解读系列答案
小学教材完全解读系列答案
相关题目
