题目内容
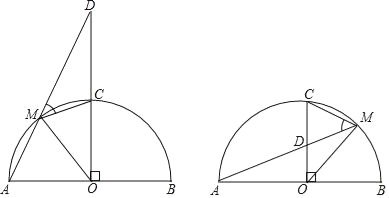
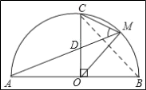
【题目】如图,AB是以O为圆心的半圆的直径,半径CO⊥AO,点M是![]() 上的动点,且不与点A、C、B重合,直线AM交直线OC于点D,连结OM与CM.
上的动点,且不与点A、C、B重合,直线AM交直线OC于点D,连结OM与CM.
(1)若半圆的半径为10.
①当∠AOM=60°时,求DM的长;
②当AM=12时,求DM的长.
(2)探究:在点M运动的过程中,∠DMC的大小是否为定值?若是,求出该定值;若不是,请说明理由.
【答案】(1)①DM= 10;②MD=![]() ;(2)∠CMD=45°.
;(2)∠CMD=45°.
【解析】
(1)①当![]() 时,所以△AMO是等边三角形,从而可知∠MOD=30°,∠D=30°,所以DM=OM=10;
时,所以△AMO是等边三角形,从而可知∠MOD=30°,∠D=30°,所以DM=OM=10;
②过点M作MF⊥OA于点F,设AF=x,![]() 利用勾股定理即可求出x的值.易证明△AMF∽△ADO,从而可知AD的长度,进而可求出MD的长度.
利用勾股定理即可求出x的值.易证明△AMF∽△ADO,从而可知AD的长度,进而可求出MD的长度.
(2)根据点M的位置分类讨论,然后利用圆周角定理以及圆内接四边形的性质即可求出答案.
(1)①当∠AOM=60°时,
∵![]()
∴△AMO是等边三角形,
∴∠A=∠MOA=60°,
∴∠MOD=30°,∠D=30°,
∴DM=OM=10
②过点M作MF⊥OA于点F,
设![]()
∴![]()
∵![]()
由勾股定理可知:![]()
∴![]()
∴![]()
∵MF∥OD,
∴△AMF∽△ADO,
∴![]()
![]()
![]()
∴![]()
∴![]()
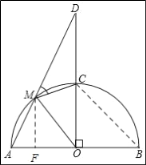
(2)当点M位于![]() 之间时,
之间时,
连接BC,
∵C是![]() 的中点,
的中点,
∴∠B=45°,
∵四边形AMCB是圆内接四边形,
此时∠CMD=∠B=45°,
当点M位于![]() 之间时,
之间时,
连接BC,
由圆周角定理可知:∠CMD=∠B=45°
综上所述,∠CMD=45°

练习册系列答案
相关题目