题目内容
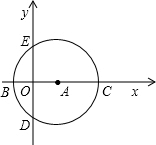
如图,在平面直角坐标系中,以点A(3,0)为圆心,以5为半径的圆与x轴相交于B、C,与y轴相交于点D、E.若抛物线y=
x2+bx+c经过C、D两点,求抛物线的解析式,并判断点B是否在抛物线上.
| 1 |
| 4 |

连接AD.
∵A(3,0),AC=5=AB,
∴C的坐标为(8,0),B的坐标为(-2,0).(2分)
∵AD=5,OA=3,∠DOA=90°,
∴OD=4.
∴点D的坐标为(0,-4).(2分)
把点D和点C的坐标代入y=
x2+bx+c,
得
,(2分)
解得b=-
,c=-4.
∴解析式为y=
x2-
x-4.(2分)
当x=-2时,y=0.(2分)
∴点B在抛物线上.(1分)
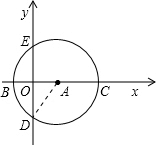
∵A(3,0),AC=5=AB,
∴C的坐标为(8,0),B的坐标为(-2,0).(2分)
∵AD=5,OA=3,∠DOA=90°,
∴OD=4.
∴点D的坐标为(0,-4).(2分)
把点D和点C的坐标代入y=
| 1 |
| 4 |
得
|
解得b=-
| 3 |
| 2 |
∴解析式为y=
| 1 |
| 4 |
| 3 |
| 2 |
当x=-2时,y=0.(2分)
∴点B在抛物线上.(1分)


练习册系列答案
相关题目


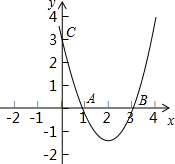
 x2)且(x1+1)(x2+1)=5
x2)且(x1+1)(x2+1)=5