题目内容
已知:如图,抛物线y=ax2+bx+c与x轴相交于两点A(1,0),B(3,0)与y轴相交于点C(0,3),
(l)求抛物线的函数关系式;
(2)若点D(4,m)是抛物线y=ax2+bx+c上一点,请求出m的值,并求出此时△ABD的面积.
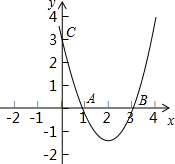
(l)求抛物线的函数关系式;
(2)若点D(4,m)是抛物线y=ax2+bx+c上一点,请求出m的值,并求出此时△ABD的面积.
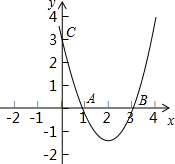
(1)把A(1,0),B(3,0),C(0,3)代入抛物线y=ax2+bx+c得:
,
把c=3代入①和②得:
,
解得:
,
∴抛物线的函数解析式为y=x2-4x+3;
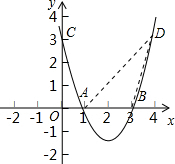
(2)把D(4,m)代入抛物线的函数解析式为y=x2-4x+3中,
得m=42-4×4+3=3,
∴S△ABD=
×(3-1)×3=3.
|
把c=3代入①和②得:
|
解得:
|
∴抛物线的函数解析式为y=x2-4x+3;
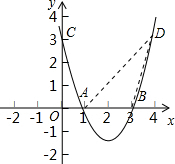
(2)把D(4,m)代入抛物线的函数解析式为y=x2-4x+3中,
得m=42-4×4+3=3,
∴S△ABD=
| 1 |
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目