ƒøƒ⁄»ð
°æƒø°ø»ÁÕº1£¨µ„![]() °¢
°¢![]() °¢
°¢![]() °¢
°¢![]() ∑÷±‘⁄æÿ–Œ
∑÷±‘⁄æÿ–Œ![]() µƒ±þ
µƒ±þ![]() °¢
°¢![]() °¢
°¢![]() °¢
°¢![]() …œ£¨
…œ£¨![]() .
.
«Û÷§£∫![]() .(
.(![]() ±Ì æ√ʪ˝)
±Ì æ√ʪ˝)

µ—ÈÃΩæø£∫
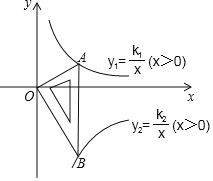
ƒ≥ ˝—ß µ—È–°◊È∑¢œ÷£∫»ÙÕº1÷–![]() £¨µ„
£¨µ„![]() ‘⁄
‘⁄![]() …œ“∆∂Ø ±£¨…œ ˆΩ·¬€ª·∑¢…˙±‰ªØ£¨∑÷±π˝µ„
…œ“∆∂Ø ±£¨…œ ˆΩ·¬€ª·∑¢…˙±‰ªØ£¨∑÷±π˝µ„![]() °¢
°¢![]() ◊˜
◊˜![]() ±þµƒ∆Ω––œþ£¨‘Ÿ∑÷±π˝µ„
±þµƒ∆Ω––œþ£¨‘Ÿ∑÷±π˝µ„![]() °¢
°¢![]() ◊˜
◊˜![]() ±þµƒ∆Ω––œþ£¨ÀƒÃı∆Ω––œþ∑÷±œýΩª”⁄µ„
±þµƒ∆Ω––œþ£¨ÀƒÃı∆Ω––œþ∑÷±œýΩª”⁄µ„![]() °¢
°¢![]() °¢
°¢![]() °¢
°¢![]() £¨µ√µΩæÿ–Œ
£¨µ√µΩæÿ–Œ![]() .
.
»ÁÕº2£¨µ±![]() ±£¨»ÙΩ´µ„
±£¨»ÙΩ´µ„![]() œÚµ„
œÚµ„![]() øøΩ¸(
øøΩ¸(![]() )£¨æ≠π˝ÃΩÀ˜£¨∑¢œ÷£∫
)£¨æ≠π˝ÃΩÀ˜£¨∑¢œ÷£∫
![]() .
.
»ÁÕº3£¨µ±![]() ±£¨»ÙΩ´µ„
±£¨»ÙΩ´µ„![]() œÚµ„
œÚµ„![]() øøΩ¸(
øøΩ¸(![]() £¨«ÎÃΩÀ˜
£¨«ÎÃΩÀ˜![]() °¢
°¢![]() ”Î
”Î![]() ÷ƺ‰µƒ ˝¡øπÿœµ£¨≤¢Àµ√˜¿Ì”….
÷ƺ‰µƒ ˝¡øπÿœµ£¨≤¢Àµ√˜¿Ì”….

«®“∆”¶”√£∫
«Î÷±Ω””¶”√°∞ µ—ÈÃΩæø°±÷–∑¢œ÷µƒΩ·¬€Ω‚¥œ¬¡–Œ Â.
(1)»ÁÕº4£¨µ„![]() °¢
°¢![]() °¢
°¢![]() °¢
°¢![]() ∑÷± «√ʪ˝Œ™25µƒ’˝∑Ω–Œ
∑÷± «√ʪ˝Œ™25µƒ’˝∑Ω–Œ![]() ∏˜±þ…œµƒµ„£¨“—÷™
∏˜±þ…œµƒµ„£¨“—÷™![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨«Û
£¨«Û![]() µƒ≥§.
µƒ≥§.

(2)»ÁÕº5£¨‘⁄æÿ–Œ![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() £¨µ„
£¨µ„![]() °¢
°¢![]() ∑÷±‘⁄±þ
∑÷±‘⁄±þ![]() °¢
°¢![]() …œ£¨
…œ£¨![]() £¨
£¨![]() £¨µ„
£¨µ„![]() °¢
°¢![]() ∑÷± «±þ
∑÷± «±þ![]() °¢
°¢![]() …œµƒ∂ص„£¨«“
…œµƒ∂ص„£¨«“![]() £¨¡¨Ω”
£¨¡¨Ω”![]() °¢
°¢![]() £¨«Î÷±Ω”–¥≥ˆÀƒ±þ–Œ
£¨«Î÷±Ω”–¥≥ˆÀƒ±þ–Œ![]() √ʪ˝µƒ◊Ó¥Û÷µ.
√ʪ˝µƒ◊Ó¥Û÷µ.

°æ¥∞∏°øŒ Â≥ œ÷£∫![]() £ª µ—ÈÃΩæø£∫
£ª µ—ÈÃΩæø£∫![]() £ª«®“∆”¶”√£∫£®1£©
£ª«®“∆”¶”√£∫£®1£©![]() £ª£®2£©
£ª£®2£©![]()
°æΩ‚Œˆ°ø
‘Â∑÷Œˆ£∫Œ Â≥ œ÷£∫∏˘æðæÿ–Œµƒ–‘÷ £¨Õ®π˝∏Ó≤π∑®¿˚”√»˝Ω«–Œµƒ√ʪ˝∫Õæÿ–Œµƒ√ʪ˝ø…µ√µΩΩ·¬€£ª
µ—ÈÃΩæø£∫”…“‚µ√£¨µ±Ω´µ„![]() œÚµ„
œÚµ„![]() øøΩ¸
øøΩ¸![]() ±£¨Õ®π˝∏Ó≤π∑®¿˚”√»˝Ω«–Œµƒ√ʪ˝∫Õæÿ–Œµƒ√ʪ˝ø…µ√µΩΩ·¬€£ª
±£¨Õ®π˝∏Ó≤π∑®¿˚”√»˝Ω«–Œµƒ√ʪ˝∫Õæÿ–Œµƒ√ʪ˝ø…µ√µΩΩ·¬€£ª
«®“∆”¶”√£∫£®1£©”……œ√ʵƒΩ·¬€£¨Ω·∫œÕº–Œ£¨Õ®π˝∏Ó≤π∑®¿˚”√»˝Ω«–Œµƒ√ʪ˝∫Õæÿ–Œµƒ√ʪ˝ø…µ√µΩΩ·¬€£ª
£®2£©÷±Ω”∏˘æðπʬ…–¥≥ˆΩ·π˚º¥ø….
‘Ã‚Ω‚Œˆ£∫Œ Â≥ œ÷£∫
“ÚŒ™Àƒ±þ–Œ![]() «æÿ–Œ£¨À˘“‘
«æÿ–Œ£¨À˘“‘![]() £¨
£¨![]() £¨
£¨
”÷“ÚŒ™![]() £¨À˘“‘Àƒ±þ–Œ
£¨À˘“‘Àƒ±þ–Œ![]() «æÿ–Œ£¨
«æÿ–Œ£¨
À˘“‘![]() £¨Õ¨¿Ìø…µ√
£¨Õ¨¿Ìø…µ√![]() .
.
“ÚŒ™![]() £¨À˘“‘
£¨À˘“‘![]() .
.
µ—ÈÃΩæø£∫
”…“‚µ√£¨µ±Ω´µ„![]() œÚµ„
œÚµ„![]() øøΩ¸
øøΩ¸![]() ±£¨
±£¨
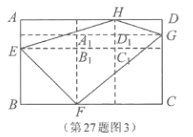
»ÁÕºÀ˘ 棨![]() £¨
£¨![]() £¨
£¨
![]() £¨
£¨![]() £¨
£¨
À˘“‘![]() £¨
£¨
À˘“‘![]() £¨
£¨
º¥![]() .
.
«®“∆”¶”√£∫
(1) »ÁÕºÀ˘ 棨”…°∞ µ—ÈÃΩæø°±µƒΩ·¬€ø…÷™![]() £¨
£¨
À˘“‘![]() £¨
£¨
“ÚŒ™’˝∑Ω–Œ√ʪ˝ «25£¨À˘“‘±þ≥§Œ™5£¨
”÷![]() £¨
£¨
À˘“‘![]() £¨
£¨![]() £¨
£¨
À˘“‘![]() £¨
£¨
À˘“‘£¨![]() .
.
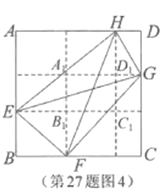
£®2£©Àƒ±þ–Œ![]() √ʪ˝µƒ◊Ó¥Û÷µŒ™
√ʪ˝µƒ◊Ó¥Û÷µŒ™![]() .
.

°æƒø°øƒ≥œÿœÏ”¶°∞Ω®…˪∑±£Ω⁄‘º–Õ…Áª·°±µƒ∫≈’Ÿ£¨æˆ∂®◊ ÷˙≤ø∑÷¥Â’Ú–ÞΩ®“ª≈˙’”∆¯≥ÿ£¨ π≈©√Ò”√µΩæ≠º√°¢ª∑±£µƒ’”∆¯ƒÐ‘¥£Æ–“∏£¥Âπ≤”–264ªß¥Â√Ò£¨’˛∏Æ≤π÷˙¥Â¿Ô34ÕÚ‘™£¨≤ª◊„≤ø∑÷”…¥Â√ÒºØ◊ £Æ–ÞΩ®A–Õ°¢B–Õ’”∆¯≥ÿπ≤20∏ˆ£Æ¡Ω÷÷–Õ∫≈’”∆¯≥ÿ√ø∏ˆ–ÞΩ®∑—”√°¢ø…π© π”√ªß ˝°¢–ÞΩ®”√µÿ«Èøˆ»Áœ¬±Ì£∫
’”∆¯≥ÿ | –ÞΩ®∑—”√£®ÕÚ‘™/∏ˆ£© | ø…π© π”√ªß ˝£®ªß/∏ˆ£© | ’ºµÿ√ʪ˝£®m2/∏ˆ£© |
A–Õ | 3 | 20 | 48 |
B–Õ | 2 | 3 | 6 |
’˛∏Æœýπÿ≤ø√≈≈˙∏¯∏√¥Â’”∆¯≥ÿ–ÞΩ®”√µÿ708∆Ω∑Ω√◊£Æ…Ë–ÞΩ®A–Õ’”∆¯≥ÿx∏ˆ£¨–ÞΩ®¡Ω÷÷–Õ∫≈’”∆¯≥ÿπ≤–Ë∑—”√yÕÚ‘™£Æ
£®1£©”√∫¨”–xµƒ¥˙ ˝ Ω±Ì æy£ª
£®2£©≤ª≥¨π˝’˛∏Æ≈˙∏¯–ÞΩ®’”∆¯≥ÿ”√µÿ√ʪ˝£¨”÷“™ π∏√¥Â√øªß¥Â√Ò”√…œ’”∆¯µƒ–ÞΩ®∑Ω∞∏”–º∏÷÷£ª
£®3£©»Ù∆Ωæ˘√øªß¥Â√ÒºØ◊ 700‘™£¨ƒÐ∑Ò¬˙◊„À˘–Ë∑—”√◊Ó…Ÿµƒ–ÞΩ®∑Ω∞∏£Æ