Question

【题目】如图,圆柱形容器中，高为120cm，底面周长为100cm，在容器内壁离容器底部40cm，的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿40cm与蚊子相对的点A处，
则壁虎捕捉蚊子的最短距离为Cm（容器厚庋忽略不计）.

Answer 1

【答案】130
【解析】解：如图,将容器侧面展开,作A关于EC的对称点A′,连接A′B交EC于F,则A′B即为最短距离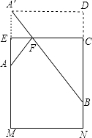
∵高为120cm，底面周长为100cm，在容器内壁离容器底部40cm的点B处有一蚊子，此时一只壁虎正好在容器外壁，离容器上沿40cm与蚊子相对的点A处，
∴A′D=50cm，BD=120cm，
∴在直角△A′DB中,A′B===130cm .
所以答案是：130 。
【考点精析】利用几何体的展开图和轴对称-最短路线问题对题目进行判断即可得到答案，需要熟知沿多面体的棱将多面体剪开成平面图形，若干个平面图形也可以围成一个多面体；同一个多面体沿不同的棱剪开，得到的平面展开图是不一样的，就是说：同一个立体图形可以有多种不同的展开图；已知起点结点，求最短路径；与确定起点相反，已知终点结点，求最短路径；已知起点和终点，求两结点之间的最短路径；求图中所有最短路径．