题目内容
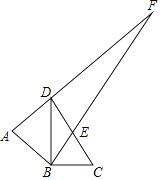
【题目】如图,在ABCD中,过点D作DE⊥BD交BA的延长线于点E.
(1)当ABCD是菱形时,证明:AE=AB;
(2)当ABCD是矩形时,设∠E=α,问:∠E与∠DOA满足什么数量关系?写出结论并说明理由.

【答案】(1)证明见解析;(2)∠E=90°﹣![]()
【解析】
(1)由四边形ABCD是菱形可得AC⊥BD,AB=CD,根据DE⊥BD,可证四边形ACDE是平行四边形,可证得结论.(2)由题意可得∠DOA=2∠OBA,∠E=90°-∠OBA,即可求∠E与∠DOA的数量关系.
证明:(1)∵四边形ABCD是菱形,
∴AC⊥BD,AB∥CD,AB=CD;
∵DE⊥BD,AC⊥BD,
∴AC∥DE,且CD∥AB,
∴四边形ACDE是平行四边形,
∴AE=CD且AB=CD,
∴AE=AB;
(2)∠E=90°﹣![]() ,
,
∵四边形ABCD是矩形,
∴AO=BO,
∴∠OBA=∠OAB;
∵DE⊥BD,∠DOA=∠OBA+∠OAB,
∴∠E=90°﹣∠OBA,∠DOA=2∠OBA,
∴∠E=90°﹣![]() .
.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
【题目】某校为了解学生平均每天课外阅读的时间,随机调查了该校部分学生一周内平均每天课外阅读的时间(以分钟为单位,并取整数),将有关数据统计整理并绘制成尚未完成的频率分布表和频数分布直方图.请你根据图表中所提供的信息,解答下列问题.
频率分布表
组别 | 分组 | 频数 | 频率 |
1 | 15~25 | 7 | 0.14 |
2 | 25~35 | a | 0.24 |
3 | 35~45 | 20 | 0.40 |
4 | 45~55 | 6 | b |
5 | 55~65 | 5 | 0.10 |
注:这里的15~25表示大于等于15同时小于25.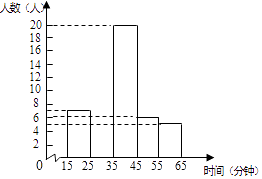
(1)求被调查的学生人数;
(2)直接写出频率分布表中的a和b的值,并补全频数分布直方图;
(3)若该校共有学生500名,则平均每天课外阅读的时间不少于35分钟的学生大约有多少名?