Question

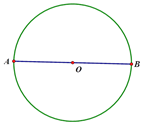
【题目】(1)尺规作图：如图，AB为⊙O的直径，过点A作⊙O的切线m;

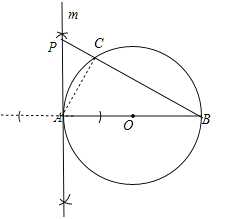
（2）在直线m上任取一点P（A点除外），连接PB交圆O与点C，请补全图形，并证明：

Answer 1

【答案】(1)见解析;(2)见解析.

【解析】（1）过点A作AB的垂线得到⊙O的切线；

（2）连接AC，利用切线的性质得AP⊥AB，再利用圆周角定理得到∠ACB=90°，接着证明△APC～△BPA，然后利用相似三角形的性质得到结论．

（1）如图，直线m为所求作；

（2）如图，证明如下：连接AC．

∵AP是⊙O的切线，∴AP⊥AB．

又∵AB为⊙O的直径，∴∠ACB=90°，∴∠ACP=∠BAP=90°．

∵∠APC=∠BPA，∴△APC～△BPA，∴PA：PC=PB：PA，∴PA2=PCPB．