题目内容
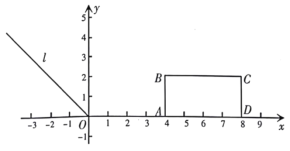
【题目】如图，在平面直角坐标系中，长方形ABCD的边AB在y轴正半轴上，顶点A的坐标为（0，2），设顶点C的坐标为（a，b）．
（1）顶点B的坐标为 ，顶点D的坐标为 （用a或b表示）；
（2）如果将一个点的横坐标作为x的值，纵坐标作为y的值，代入方程2x+3y＝12成立，就说这个点的坐标是方程2x+3y＝12的解．已知顶点B和D的坐标都是方程2x+3y＝12的解，求a，b的值；
（3）在（2）的条件下，平移长方形ABCD，使点B移动到点D，得到新的长方形EDFG，
①这次平移可以看成是先将长方形ABCD向右平移 个单位长度，再向下平移 个单位长度的两次平移；
②若点P（m，n）是对角线BD上的一点，且点P的坐标是方程2x+3y＝12的解，试说明平移后点P的对应点P′的坐标也是方程2x+3y＝12的解．
【答案】（1）（0，b），（a，2）；（2）
；（3）①3，2；②P′的坐标也是方程2x+3y＝12的解．
【解析】
（1）由题意，结合长方形的性质可得点B和点D的坐标；
（2）因为点B和D的坐标都是方程2x+3y＝12的解，则将B、D两点坐标带入方程2x+3y＝12，得到方程组，求解即可得到答案.
（3）①本题考查平移，利用平移的性质可以得到答案；
②将点P的坐标和P′的坐标代入方程2x+3y＝12，若两者相等，即可证明.
（1）由A的坐标为（0，2），C的坐标为（a，b），以及长方形ABCD的性质可知，
AB=b,AD=a,则B（0，b），D（a，2），
故答案为（0，b），（a，2）；
（2）∵顶点B和D的坐标都是方程2x+3y＝12的解，
∴
，
解得
．
（3）在（2）的条件下，平移长方形ABCD，使点B移动到点D，得到新的长方形EDFG，
①这次平移可以看成是先将长方形ABCD向右平移3个单位长度，再向下平移2个单位长度的两次平移；
故答案为3，2；
②点P（m，n）平移后的坐标为（m+3，n﹣2），
∵点P的坐标是方程2x+3y＝12的解，
∴2m+3n＝12，
将P′的坐标代入方程2x+3y＝12， 2（m+3）+3（n﹣2）＝2m+3n＝12，
∴P′的坐标也是方程2x+3y＝12的解．
