题目内容
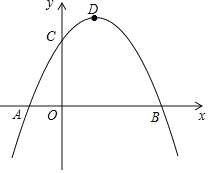
【题目】如图,在平面直角坐标系中,矩形OADB的顶点A,B的坐标分别为A(﹣6,0),B(0,4).过点C(﹣6,1)的双曲线y=![]() (k≠0)与矩形OADB的边BD交于点E.
(k≠0)与矩形OADB的边BD交于点E.
(1)填空:OA= ,k= ,点E的坐标为 ;
(2)当1≤t≤6时,经过点M(t﹣1,﹣![]() t2+5t﹣
t2+5t﹣![]() )与点N(﹣t﹣3,﹣
)与点N(﹣t﹣3,﹣![]() t2+3t﹣
t2+3t﹣![]() )的直线交y轴于点F,点P是过M,N两点的抛物线y=﹣
)的直线交y轴于点F,点P是过M,N两点的抛物线y=﹣![]() x2+bx+c的顶点.
x2+bx+c的顶点.
①当点P在双曲线y=![]() 上时,求证:直线MN与双曲线y=
上时,求证:直线MN与双曲线y=![]() 没有公共点;
没有公共点;
②当抛物线y=﹣![]() x2+bx+c与矩形OADB有且只有三个公共点,求t的值;
x2+bx+c与矩形OADB有且只有三个公共点,求t的值;
③当点F和点P随着t的变化同时向上运动时,求t的取值范围,并求在运动过程中直线MN在四边形OAEB中扫过的面积.

【答案】(1)6,﹣6,(﹣![]() ,4);(2)①证明见解析;②t=
,4);(2)①证明见解析;②t=![]() 或t=
或t=![]() ;③
;③![]() .
.
【解析】(1)根据题意将相关数据代入.
(2)①用t表示直线MN解析式,及b,c,得到P点坐标带入双曲线y=![]() 解析式,证明关于t的方程无解即可;
解析式,证明关于t的方程无解即可;
②根据抛物线开口和对称轴,分别讨论抛物线过点B和在BD上时的情况;
③由②中部分结果,用t表示F、P点的纵坐标,求出t的取值范围及直线MN在四边形OAEB中所过的面积.
解:(1)∵A点坐标为(﹣6,0)
∴OA=6
∵过点C(﹣6,1)的双曲线y=![]()
∴k=﹣6
y=4时,x=![]()
∴点E的坐标为(﹣![]() ,4)
,4)
故答案为:6,﹣6,(﹣![]() ,4)
,4)
(2)①设直线MN解析式为:y1=k1x+b1
由题意得:
解得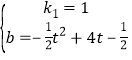 ,
,
∵抛物线y=﹣![]() 过点M、N,
过点M、N,
∴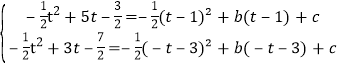 ,
,
解得![]()
∴抛物线解析式为:y=﹣![]() x2﹣x+5t﹣2
x2﹣x+5t﹣2
∴顶点P坐标为(﹣1,5t﹣![]() )
)
∵P在双曲线y=﹣![]() 上
上
∴(5t﹣![]() )×(﹣1)=﹣6
)×(﹣1)=﹣6
∴t=![]()
此时直线MN解析式为:
联立
∴8x2+35x+49=0
∵△=352﹣4×8×48=1225﹣1536<0
∴直线MN与双曲线y=﹣![]() 没有公共点.
没有公共点.
②当抛物线过点B,此时抛物线y=﹣![]() x2+bx+c与矩形OADB有且只有三个公共点
x2+bx+c与矩形OADB有且只有三个公共点
∴4=5t﹣2,得t=![]()
当抛物线在线段DB上,此时抛物线与矩形OADB有且只有三个公共点
∴![]() ,得t=
,得t=![]()
∴t=![]() 或t=
或t=![]()
③∵点P的坐标为(﹣1,5t﹣![]() )
)
∴yP=5t﹣![]()
当1≤t≤6时,yP随t的增大而增大
此时,点P在直线x=﹣1上向上运动
∵点F的坐标为(0,﹣![]() )
)
∴yF=﹣![]()
∴当1≤t≤4时,随者yF随t的增大而增大
此时,随着t的增大,点F在y轴上向上运动
∴1≤t≤4
当t=1时,直线MN:y=x+3与x轴交于点G(﹣3,0),与y轴交于点H(0,3)
当t=4﹣![]() 时,直线MN过点A.
时,直线MN过点A.
当1≤t≤4时,直线MN在四边形AEBO中扫过的面积为
S=![]() .
.

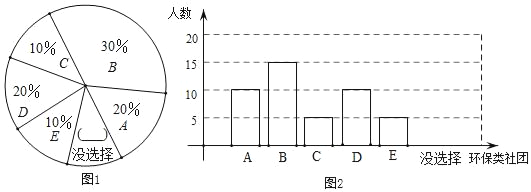
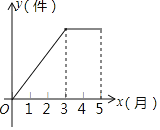
【题目】某校创建“环保示范学校”,为了解全校学生参加环保类杜团的意愿,在全校随机抽取了50名学生进行问卷调查,问卷给出了五个社团供学生选择(学生可根据自己的爱好选择一个社团,也可以不选),对选择了社团的学生的问卷情况进行了统计,如表:
社团名称 | A.酵素制作社团 | B.回收材料小制作社团 | C.垃圾分类社团 | D.环保义工社团 | E.绿植养护社团 |
人数 | 10 | 15 | 5 | 10 | 5 |
(1)填空:在统计表中,这5个数的中位数是 ;
(2)根据以上信息,补全扇形图(图1)和条形图(图2);
(3)该校有1400名学生,根据调查统计情况,请估计全校有多少学生愿意参加环保义工社团;
(4)若小诗和小雨两名同学在酵素制作社团或绿植养护社团中任意选择一个参加,请用树状图或列表法求出这两名同学同时选择绿植养护社团的概率.