题目内容
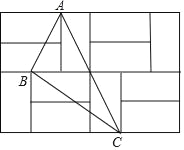
【题目】如图,由12个形状、大小完全相同的小矩形组成一个大的矩形网格,小矩形的顶点称为这个矩形网格的格点,已知这个大矩形网格的宽为6,△ABC的顶点都在格点.
(1)求每个小矩形的长与宽;
(2)在矩形网格中找一格点E,使△ABE为直角三角形,求出所有满足条件的线段AE的长度.
(3)求sin∠BAC的值.
【答案】(1)每个小矩形的长为3,宽为1.5;(2)3或3![]() 或
或![]() ;(3)
;(3)![]() .
.
【解析】(1)设每个小矩形的长为x,宽为y,根据图形可知小矩形的长与宽间的数量关系有两个:2个矩形的宽=矩形的长;两个矩形的宽+1个矩形的长=6,据此列出方程组,并解答即可;
(2)利用图形和勾股定理逆定理进行解答;
(3)过B作BP⊥AC于P,则BM=MN=y,AM=2y, AB=AN=![]() .由S△ABN=
.由S△ABN=![]() BN×AM=
BN×AM=![]() AN×BP,得到BP的长.在Rt△ABP中, 利用正弦的定义求解即可.
AN×BP,得到BP的长.在Rt△ABP中, 利用正弦的定义求解即可.
(1)设每个小矩形的长为x,宽为y,依题意得:![]() ,解得:
,解得:![]() ,所以每个小矩形的长为3,宽为1.5;
,所以每个小矩形的长为3,宽为1.5;
(2)如图所示:
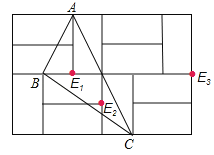
AE=3或3![]() 或
或![]() ;
;
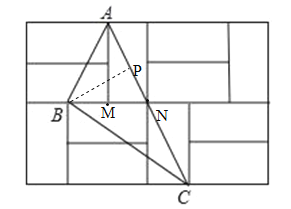
(3)如图,过B作BP⊥AC于P,则BM=MN=y,AM=2y.
∵AM⊥BN,∴AB=AN=![]() =
=![]() .
.
∵S△ABN=![]() BN×AM=
BN×AM=![]() AN×BP,∴BP=
AN×BP,∴BP=![]() =
=![]() =
=![]() .在Rt△ABP中, sin∠BAC =sin∠BAP=
.在Rt△ABP中, sin∠BAC =sin∠BAP=![]() =
=![]() ÷
÷![]() =
=![]() .
.

练习册系列答案
相关题目