题目内容
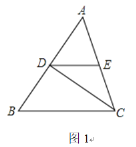
【题目】已知△ABC中,∠ACB的平分线CD交AB于点D,DE∥BC,
(1)如果点E是边AC的中点,AC=5cm,求DE的长;
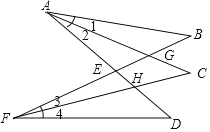
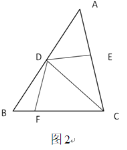
(2)如图2,若DE平分∠ADC,在BC边上取点F,使∠DFC=60°,若BC=7,BF=2,求DF的长.
【答案】(1)DE=2.5cm;(2)DF=3.
【解析】
(1)根据角平分线定义得到∠BCD =∠ACD,由于DE∥BC,根据平行线性质得∠EDC =∠BCD,则∠EDC =∠ACD,然后可得ED=EC,由点E是边AC的中点,AC=5cm得EC=2.5cm,所以DE=2.5cm;
(2)作DG⊥BC于点G,易求GB、GF的长,再根据在直角三角形中30°的锐角所对的直角边是斜边的一半即可求出DF的长.
解:(1)∵CD平分∠ACB,
∴∠BCD =∠ACD,
∵DE∥BC,
∴∠EDC =∠BCD,
∴∠EDC =∠ACD,
∴ED=EC,
∵点E是边AC的中点,AC=5cm,
∴EC=2.5cm,
∴DE=2.5cm;
(2)作DG⊥BC于点G,

∵DE∥BC,
∴∠ADE=∠B,∠EDC=∠DCB,
∵DE平分∠ADC,
∴∠ADE=∠EDC,
∴∠B=∠DCB,
∴DB=DC.
∵DG⊥BC,
∴GB=![]() BC=
BC=![]() ×7=3.5,
×7=3.5,
∴GF=GBBF=3.52=1.5,
∵Rt△DGF中,∠DFG=60°,
∴∠FDG=30°
∴DF=2GF=2×1.5=3.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目