题目内容
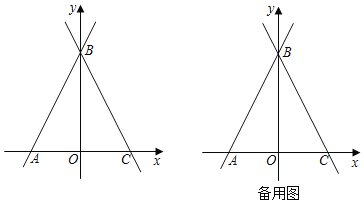
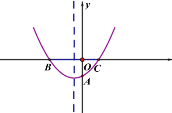
【题目】如图,二次函数y=ax2+bx+c 的图象与 x 轴交于 B、C 两点,交 y 轴于点 A.
(1)根据图象请用“>”、“<”或“=”填空:a 0,b 0,c 0;
(2)如果 OC=OA=![]() OB,BC=3,求这个二次函数的解析式;
OB,BC=3,求这个二次函数的解析式;
(3) 在(2)中抛物线的对称轴上,存在点 Q 使得△OQA 的周长最短,试求出点 Q 的坐标.
【答案】(1)a>0,b>0,c<0; (2)y=![]() x2+
x2+![]() x-1;(3)Q(-
x-1;(3)Q(-![]() ,
,![]() ).
).
【解析】
(1)根据抛物线开口方向、对称轴方程以及抛物线与y轴交点的位置确定a,b,c的符号;
(2)首先由函数图象可确定A,B,C三点的坐标,然后分别代入二次函数y=ax2+bx+c中即可解得系数,进而即得解析式.
(3)设O关于对称轴的对称点为D,连接AD交对称轴于点Q,求出直线AD的解析式,把对称轴x=-![]() 即可求出Q的坐标.
即可求出Q的坐标.
解:(1)如图,∵抛物线开口方向向上,
∴a>0.
又∵对称轴x=-![]() <0,
<0,
∴a、b同号,即b>0.
∵抛物线与y轴交与负半轴,
∴c<0.
综上所述,a>0,b>0,c<0.
(2)∵OC=OA=![]() OB,BC=3,
OB,BC=3,
∴点A的坐标为(0,-1),点B的坐标为(-2,0),点C的坐标为(1,0),
把A,B,C三点分别代入二次函数y=ax2+bx+c中可得:
 ,
,
解得 ,
,
∴该二次函数的解析式是:y=![]() x2+
x2+![]() x-1;
x-1;
(3)如图,设O关于对称轴的对称点为D,连接AD交对称轴于点Q,

对于y=![]() x2+
x2+![]() x-1,其对称轴为:直线x=-
x-1,其对称轴为:直线x=-![]() ,
,
∵O关于对称轴的对称点为D,
∴D(-1,0),
设直线AD的解析式为y=kx+b,把D(-1,0),A(0,-1)代入得
![]() ,解得
,解得![]() ,
,
∴y=-x-1,
当x=-![]() 时,y=
时,y=![]() ,
,
∴Q(-![]() ,
,![]() ).
).

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目