题目内容
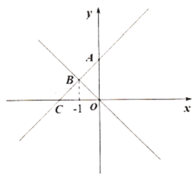
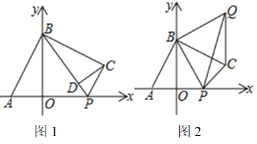
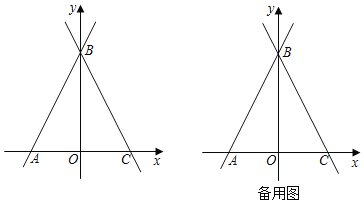
【题目】如图，在平面直角坐标系中，直线y＝2x+6与x轴交于点A，与y轴交于点B，过点B的直线交x轴于点C，且AB＝BC．
（1）求直线BC的解析式；
（2）点P为线段AB上一点，点Q为线段BC延长线上一点，且AP＝CQ，设点Q横坐标为m，求点P的坐标（用含m的式子表示，不要求写出自变量m的取值范围）；
（3）在（2）的条件下，点M在y轴负半轴上，且MP＝MQ，若∠BQM＝45°，求直线PQ的解析式．
【答案】（1）y＝﹣2x+6；（2）点P（m﹣6，2m﹣6）；（3）y＝﹣x+
【解析】
（1）先求出点A，点B坐标，由等腰三角形的性质可求点C坐标，由待定系数法可求直线BC的解析式；
（2）证明△PGA≌△QHC（AAS），则PG＝HQ＝2m﹣6，故点P的纵坐标为：2m﹣6，而点P在直线AB上，即可求解；
（3）由“SSS”可证△APM≌△CQM，△ABM≌△CBM，可得∠PAM＝∠MCQ，∠BQM＝∠APM＝45°，∠BAM＝∠BCM，由“AAS”可证△APE≌△MAO，可得AE＝OM，PE＝AO＝3，可求m的值，进而可得点P，点Q的坐标，即可求直线PQ的解析式．
（1）∵直线y＝2x+6与x轴交于点A，与y轴交于点B，
∴点B(0，6)，点A(﹣3，0)，
∴AO＝3，BO＝6，
∵AB＝BC，BO⊥AC，
∴AO＝CO＝3，
∴点C(3，0)，
设直线BC解析式为：y＝kx+b，则
，解得：
，
∴直线BC解析式为：y＝﹣2x+6；
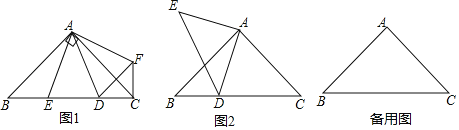
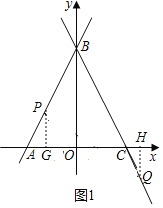
（2）如图1，过点P作PG⊥AC于点G，过点Q作HQ⊥AC于点H，
∵点Q横坐标为m，
∴点Q(m，﹣2m+6)，
∵AB＝CB，
∴∠BAC＝∠BCA＝∠HCQ，
又∵∠PGA＝∠QHC＝90°，AP＝CQ，
∴△PGA≌△QHC（AAS），
∴PG＝HQ＝2m﹣6，
∴点P的纵坐标为：2m﹣6，
∵直线AB的表达式为：y＝2x+6，
∴2m﹣6＝2x+6，解得：x＝m﹣6，
∴点P(m﹣6，2m﹣6)；
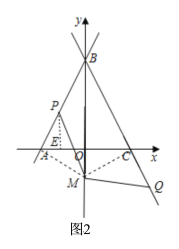
（3）如图2，连接AM，CM，过点P作PE⊥AC于点E，
∵AB＝BC，BO⊥AC，
∴BO是AC的垂直平分线，
∴AM＝CM，且AP＝CQ，PM＝MQ，
∴△APM≌△CQM（SSS）
∴∠PAM＝∠MCQ，∠BQM＝∠APM＝45°，
∵AM＝CM，AB＝BC，BM＝BM，
∴△ABM≌△CBM（SSS）
∴∠BAM＝∠BCM，
∴∠BCM＝∠MCQ，且∠BCM+∠MCQ＝180°，
∴∠BCM＝∠MCQ＝∠PAM＝90°，且∠APM＝45°，
∴∠APM＝∠AMP＝45°，
∴AP＝AM，
∵∠PAO+∠MAO＝90°，∠MAO+∠AMO＝90°，
∴∠PAO＝∠AMO，且∠PEA＝∠AOM＝90°，AM＝AP，
∴△APE≌△MAO（AAS）
∴AE＝OM，PE＝AO＝3，
∴2m﹣6＝3，
∴m＝
，
∴Q(，﹣3)，P(﹣，3)，
设直线PQ的解析式为：y＝ax+c，
∴
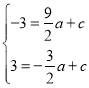，解得：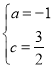
，
∴直线PQ的解析式为：y＝﹣x+．
