Question

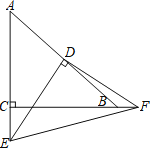
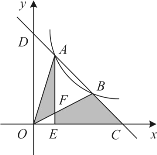
【题目】（1）如图（1），△ABC和△AOD都是等腰直角三角形，∠BAC=∠EAD=90°，点B在线段AE上，点C在线段AD上，请直接写出线段BE与线段CD的数量关系与位置关系；

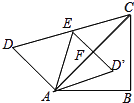
（2）如图（2），将图（1）中的△ABC绕点A顺时针施转α（0°＜α＜360°），那么（1）中线段BE与线段CD的关系是否还成立？如果成立，请你结合图（2）给出的情形进行证明；如果不成立，说明理由．

Answer 1

【答案】（1）详见解析；（2）（1）中结论成立，证明详见解析.

【解析】

（1）根据等腰直角三角形的性质可得AB=AC，AE=AD，再根据等量关系可得线段BE与线段CD的关系；

（2）根据等腰直角三角形的性质可得AB=AC，AE=AD，根据旋转的性质可得∠BAE=∠CAD，根据SAS可证△BAE≌△CAD，根据全等三角形的性质即可求解；

解：（1）∵△ABC和△AED都是等腰直角三角形，∠BAC=∠EAD=90°，

∴AB=AC，AE=AD，BE⊥CD，

∴AE-AB=AD-AC，

∴BE=CD；

（2）（1）中结论成立，

理由：如图，

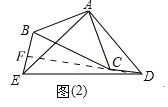
∵△ABC和△AED都是等腰直角三角形，∠BAC=∠EAD=90°，

∴AB=AC，AE=AD，

由旋转的性质得，∠BAE=∠CAD，

在△BAE与△CAD中，

，

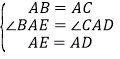∴△BAE≌△CAD（SAS）

∴BE=CD；∠AEB=∠ADC，

∴∠BED+∠EDF=∠AED+∠AEB+∠EDF=∠AED+∠ADC+∠EDF=∠AED+∠ADE=90°，

∴∠EFD=90°，

即：BE⊥CD