题目内容
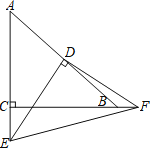
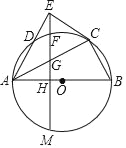
【题目】如图,AB是⊙O的直径,点D在⊙O上,∠BAD的平分线交⊙O于点C,过点C作CE⊥AD于点E,过点E作EH⊥AB于点H,交AC于点G,交⊙O于点F、M,连接BC.
(1)求证:EC是⊙O的切线;
(2)若AG=GC,试判断AG与GH的数量关系,并说明理由;
(3)在(2)的条件下,若⊙O的半径为4,求FM的长.
【答案】(1)见解析;(2)AG=2GH,理由见解析;(3)2![]() .
.
【解析】
(1)连接OC,求出OC∥AE,求出EC⊥OC,根据切线的判定得出即可;
(2)求出△EGC是等边三角形,求出∠EGC=60°,求出∠OAC=30°,即可得出答案;
(3)连接OF,根据垂径定理求出FM=2FH,根据勾股定理求出AH,求出OH,根据勾股定理求出FH,即可得出答案.
(1)证明:连接OC,
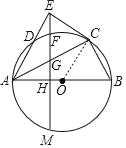
∵OA=OC,
∴∠ACO=∠OAC,
∵AC平分∠DAB,
∴∠OAC=∠DAC,
∴∠DAC=∠OCA,
∴OC∥AE,
∵CE⊥AE,
∴CE⊥OC,
∵OC过O,
∴EC是⊙O的切线;
(2)解:AG=2GH,
理由是:∵CE是⊙O切线,
∴∠OCE=90°,
∴∠OCA+∠ECA=90°,
∵EM⊥AB,
∴∠EHA=∠EHO=90°,
∴∠OAC+∠AGH=90°,
∵∠OAC=∠OCA,
∴∠AGH=∠ECA,
∵∠EGC=∠AGH,
∴∠EGC=∠ECG,
∴EC=EG,
∵∠AEC=90°,AG=GC=![]() AC,
AC,
∴EG=![]() AC,
AC,
∴EC=![]() AC,
AC,
∴EG=EC=CG,
∴△EGC是等边三角形,
∴∠EGC=60°,
∴∠AGH=∠EGC=60°,
∴∠OAC=30°,
∵∠GHA=90°,
∴AG=2GH;
(3)解:连接OF,
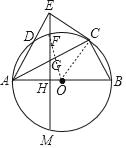
∵AB是直径,
∴∠ACB=90°,AB=2OA=2×4=8,
∵∠OAC=30°,
∴BC=![]() AB=4,
AB=4,
在Rt△ACB中,AC=![]() =
=![]() =4
=4![]() ,
,
∵AG=![]() AC,
AC,
∴AG=2![]() ,
,
∵AG=2GH,
∴GH=![]() ,
,
在Rt△AGH中,AH=![]() =
=![]() =3,
=3,
∴OH=OA﹣AH=4﹣3=1,
在Rt△FHO中,FH=![]() =
=![]() =
=![]() ,
,
由垂径定理得:PM=2FH=2![]() .
.

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案