题目内容
Rt△AOB中,∠AOB=90°,∠ABO=30°,BO=4,分别以OA,OB边所在的直线建立平面直角坐标系,D点为x轴正半轴上的一点,以OD为一边在第一象限内做等边△ODE.
(1)如图(1),当E点恰好落在线段AB上,求E点坐标;
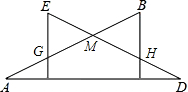
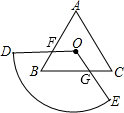
(2)在(1)问的条件下,将△ODE在线段OB上向右平移如图,图中是否存在一条与线段OO′始终相等的线段?如果存在,请指出这条线段,并加以证明;如果不存在,请说明理由;
(3)若点D从原点出发沿x轴正方向移动,设点D到原点的距离为x,△ODE与△AOB重叠部分的面积为y,请直接写出y与x的函数关系式,并写出自变量x的取值范围.
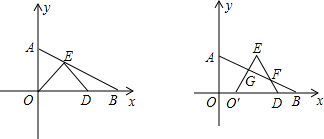
(1)如图(1),当E点恰好落在线段AB上,求E点坐标;
(2)在(1)问的条件下,将△ODE在线段OB上向右平移如图,图中是否存在一条与线段OO′始终相等的线段?如果存在,请指出这条线段,并加以证明;如果不存在,请说明理由;
(3)若点D从原点出发沿x轴正方向移动,设点D到原点的距离为x,△ODE与△AOB重叠部分的面积为y,请直接写出y与x的函数关系式,并写出自变量x的取值范围.
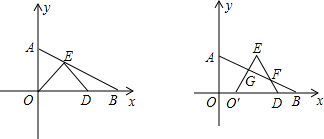
(1)作EH⊥OB于点H,
∵△OED是等边三角形,
∴∠EOD=60°.
又∵∠ABO=30°,
∴∠OEB=90°.
∵BO=4,
∴OE=
OB=2.
∵△OEH是直角三角形,且∠OEH=30°
∴OH=1,EH=
.
∴E(1,
).
(2)存在线段EF=OO'.
∵∠ABO=30°,∠EDO=60°
∴∠ABO=∠DFB=30°,
∴DF=DB.
∴OO′=4-2-DB=2-DB=2-DF=ED-FD=EF
(3)所求函数关系式为:
当0<x≤2时,△ODE与△AOB重叠部分的面积为△ODE面积,
当2<x<4时,△ODE与△AOB重叠部分的面积为四边形GO′DF面积,
当x≥4时,△ODE与△AOB重叠部分的面积为定值,
y=
.
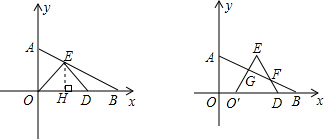
∵△OED是等边三角形,
∴∠EOD=60°.
又∵∠ABO=30°,
∴∠OEB=90°.
∵BO=4,
∴OE=
| 1 |
| 2 |
∵△OEH是直角三角形,且∠OEH=30°
∴OH=1,EH=
| 3 |
∴E(1,
| 3 |
(2)存在线段EF=OO'.
∵∠ABO=30°,∠EDO=60°
∴∠ABO=∠DFB=30°,
∴DF=DB.
∴OO′=4-2-DB=2-DB=2-DF=ED-FD=EF
(3)所求函数关系式为:
当0<x≤2时,△ODE与△AOB重叠部分的面积为△ODE面积,
当2<x<4时,△ODE与△AOB重叠部分的面积为四边形GO′DF面积,
当x≥4时,△ODE与△AOB重叠部分的面积为定值,
y=
|

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目