题目内容
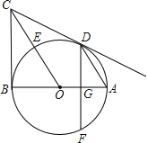
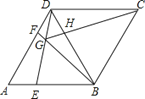
【题目】已知:△ABC是等边三角形,点D是△ABC(包含边界)平面内一点,连接CD,将线段CD绕C逆时针旋转60°得到线段CE,连接BE,DE,AD,并延长AD交BE于点P.
(1)观察填空:当点D在图1所示的位置时,填空:
①与△ACD全等的三角形是______.
②∠APB的度数为______.
(2)猜想证明:在图1中,猜想线段PD,PE,PC之间有什么数量关系?并证明你的猜想.
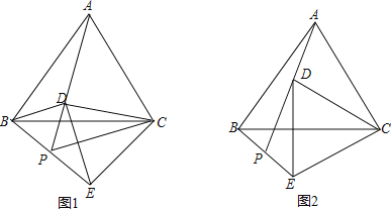
(3)拓展应用:如图2,当△ABC边长为4,AD=2时,请直接写出线段CE的最大值.
【答案】(1)①△BCE;②60°;(2)PD+PE=PC,证明见解析;(3)CE的最大值为6.
【解析】
(1)①根据旋转的性质和等边三角形的性质以及全等三角形的判定证明即可;
②根据全等三角形的判定和性质以及三角形内角和解答即可;
(2)根据等边三角形的性质以及全等三角形的判定和性质解答即可;
(3)由(1)可得CE=CD,根据D点在线段AC上,CD长度最小;D点在CA的延长线上,CD的长度最大,求出CD的最大值即可求得线段CE的最大值.
(1)①如图1中,
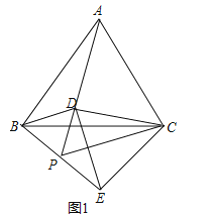
∵△ABC是等边三角形,
∴AB=AC=BC,∠BAC=∠ACB=∠ABC=60°,
∵将线段CD绕C顺时针旋转60°得到线段CE,
∴CE=CD,∠DCE=60°,
∴△DCE是等边三角形,
∴∠DCE═60°,
∵∠ACD+∠DCB=60°,∠BCE+∠DCB=60°,
∴∠ACD=∠BCE,
∴△ACD≌△BCE(SAS).
故答案为:△BCE.
②∵△ACD≌△BCE,
∴∠EBC=∠DAC,
∵∠DAC+∠BAD=∠BAC=60°,
∴∠PBC+∠BAD=60°,
∴∠APB=180°-∠ABC+∠PBC+∠BAP=180°-60°-60°=60°;
故答案为:60°.
(2)结论:PD+PE=PC.
理由:∵△ACD≌△BCE,
∴∠CBE=∠CAD,
∵∠CAD+∠BAD=60°,∠BAD+∠DBC=60°,
∴∠BAD+∠ABD=∠BDP=60°,
∵∠APB=60°,
∴△BDP是等边三角形,
∴DP=BP,
∴PD+PE=BE,
∵△ADC≌△BEC,
∴AD=BE,
∵在△ABD与△CBP中
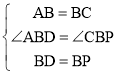 ,
,
∴△ABD≌△CBP(SAS),
∴AD=PC,
∴PD+PE=PC;
(3)如图2中,
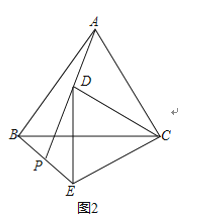
∵AC=4,AD=2,
∴D点在线段AC上,CD长度最小;D点在CA的延长线上,CD的长度最大,
∴4-2≤CD≤4+2,
∴2≤CD≤6.
∴CD的最大值为6,
由(1)可知△ACD≌△BCE,EC=CD,
∴EC的最大值为6.

 53随堂测系列答案
53随堂测系列答案【题目】如表是一个4×4(4行4列共16个“数”组成)的奇妙方阵,从这个方阵中选四个“数”,而且这四个“数”中的任何两个不在同一行,也不在同一列,有很多选法,把每次选出的四个“数”相加,其和是定值,则方阵中第三行三列的“数”是( )
30 |
| 2 | 22 |
﹣3 | ﹣2 | ﹣ | 0 |
|﹣5| | 6 | 23 | |
( | 4 |
| ( |
A. 5 B. 6 C. 7 D. 8