题目内容
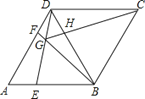
【题目】如图,四边形ABCD为菱形,AB=BD,点B、C、D、G四个点在同一个圆⊙O上,连接BG 并延长交AD于点F,连接DG并延长交AB于点E,BD与CG交于点H,连接FH,下列结 论:①AE=DF;②FH∥AB;③△DGH∽△BGE;④当CG为⊙O的直径时,DF=AF.其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
【答案】D
【解析】∵四边形ABCD为菱形,AB=BD,∴△ABD是等边三角形,∵B,C,D,G四个点在同一个⊙O上,∴∠GDC+∠GBC=180°,又∠BDC=∠DBC=60°,∴∠GDB+∠GBD=60°,又∠ADE+∠EDB=60°,∴∠ADE=∠DBF.在△ADE和△DBF中,∠A=∠ADB,AD=DB,∠ADE=∠DBF,∴△ADE≌△DBF,∴AE=DF,故①正确;∵B,C,D,G四个点在同一个⊙O上,∴∠DCG=∠DBG,又∠DBG=∠ADE,
∴∠ADE=∠DCG.在△ADE和△CDH中,∠A=∠BDC,AD=DC,∠ADE=∠DCG,∴△ADE≌△DCH,∴AE=DH,又DF=AE,∴DF=DH.又∠ADB=60°,∴∠DFH=60°,∴FH∥AB,故②正确;由△ADE≌△DCH,得∠AED=∠DHC,∴∠DHG=∠DEB,又∠ADE=∠DBG,∴∠EDB=∠FBE,∴△DGH∽△BGE,故③正确;当CG为⊙O的直径时,∠GBD=30°,又∠ADB=60°,∠DFB=90°,∵△ADB是等边三角形,∴DF=AF,故④正确.故选D.

【题目】某学习小组13名学生的一次英语听力测试成绩分布如下表所示(满分20分):
成绩(分) | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
人数(人) | 1 | 3 | 2 | 2 | 1 | 2 | 2 |
这13名学生听力测试成绩的中位数是( )
A.16分
B.17分
C.18分
D.19分