题目内容
【题目】如图，菱形ABCD的边长为1，∠ABC＝120°，E、F、P分别是AB、BC、AC上的动点，则PE+PF的最小值为_____．
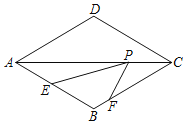
【答案】
．
【解析】
先找出点E关于AC的对称点E′，过点E′作E′F⊥BC于F，交AC于P，根据轴对称确定最短路线问题以及垂线段最短可知E′F为PE+PF的最小值，过点B作BG⊥AD于G，解直角三角形求出BG，再根据平行线间的距离相等即可得解．
解：如图，
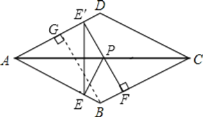
点E关于AC的对称点E′，过点E′作E′F⊥BC于F，交AC于P，
则PE+PF＝E′F为最小值的情况，
过点B作BG⊥AD于G，
∵AB＝1，∠ABC＝120°，
∴∠DAB＝60°，
∴BG＝ABsin60°＝1×＝，
∵AD∥BC，
∴E′F＝BG＝．
故答案为：．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
