题目内容
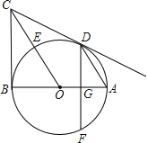
【题目】如图,AB是⊙O的直径,BC⊥AB于点B,连接OC交⊙O于点E,弦AD∥OC,弦DF⊥AB于点G.
(1)求证:点E是![]() 的中点;
的中点;
(2)求证:CD是⊙O的切线;
(3)若sin∠BAD=![]() ,⊙O的半径为5,求DF的长.
,⊙O的半径为5,求DF的长.
【答案】(1)见解析 (2)见解析 (3)![]()
【解析】
(1) 连接OD,根据平行的性质得到∠A=∠COB,再证明∠DOC=∠BOC即可得到答案;
(2)先根据题意的大△COD≌△COB,再根据全等三角形的性质以及BC⊥AB于点B即可证明;
(3)先根据sin∠BAD=![]() ,设DG=4x,AD=5x再根据勾股定理求解即可得到答案;
,设DG=4x,AD=5x再根据勾股定理求解即可得到答案;
(1)证明:连接OD,
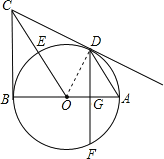
∵AD∥OC,
∴ ∠A=∠COB(两直线平行,同位角相等),
又∵∠A=![]() ∠BOD(同弧圆心角等于圆周角的2倍),
∠BOD(同弧圆心角等于圆周角的2倍),
∴∠BOC=![]() ∠BOD;
∠BOD;
∴∠DOC=∠BOC;
∴![]() ,则点E是
,则点E是![]() 的中点;
的中点;
(2)证明:如图所示:

由(1)知∠DOE=∠BOE,
∵CO=CO,OD=OB,
∴ △COD≌△COB;
∴∠CDO=∠B;
又∵BC⊥AB,
∴ ∠CDO=∠B=90°;
∴CD是⊙O的切线;
(3)解:在△ADG中,
∵sin∠BAD=![]() ,
,
设DG=4x,AD=5x;
∵ DF⊥AB,
∴ AG=3x;
又∵⊙O的半径为5,
∴ OG=5﹣3x;
∵ OD2=DG2+OG2,
∴![]() ,
,
∴ x1=![]() ,x2=0;(舍去)
,x2=0;(舍去)
∴ DF=2DG=2×4x=8x=![]() ;
;

 阅读快车系列答案
阅读快车系列答案【题目】2020年4月是我国第32个爱国卫生月.某校九年级通过网课举行了主题为“防疫有我,爱卫同行”的知识竞赛活动.为了解全年级500名学生此次竞赛成绩(百分制)的情况,随机抽取了部分参赛学生的成绩,整理并绘制出如下不完整的统计表(表1)和统计图(如图).请根据图表信息解答以下问题:
(1)本次调查一共随机抽取了____个参赛学生的成绩;
(2)表1中a=__;
(3)所抽取的参赛学生的成绩的中位数落在的“组别”是__;
(4)统计图中B组所占的百分比是_______;
(5)请你估计,该校九年级竞赛成绩达到80分以上(含80分)的学生人数.
表1 知识竞赛成绩分组统计表
组别 | 分数/分 | 频数 |
A | 60≤x<70 | a |
B | 70≤x<80 | 10 |
C | 80≤x<90 | 14 |
D | 90≤x<100 | 18 |