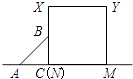题目内容
【题目】在等腰△ABC中,AD⊥BC交直线BC于点D,若AD=![]() BC,则△ABC的顶角的度数为:________
BC,则△ABC的顶角的度数为:________
【答案】30![]()
【解析】分析:分点A是顶角顶点和点A是底角顶点两种情况求解;点A是底角顶点再分△ABC为钝角三角形和锐角三角形两种情况求解.
详解:
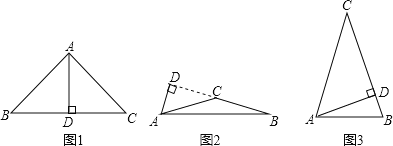
①如图1,点A是顶点时,∵AB=AC,AD⊥BC,
∴BD=CD,
∵AD=![]() BC,
BC,
∴AD=BD=CD,
在Rt△ABD中,∠C=∠B=∠BAD=![]() (180°-90°)=45°,
(180°-90°)=45°,
∴∠BAC=90°;
②如图2,点A是底角顶点,且AD在△ABC外部时,
∵AD=![]() BC,AC=BC,
BC,AC=BC,
∴AD=![]() AC,
AC,
∴∠ACD=30°,
∴∠ACB =180°-∠ACD=180°-30°=150°;
③如图3,点A是底角顶点,且AD在△ABC内部时,
∵AD=![]() BC,AC=BC,
BC,AC=BC,
∴AD=![]() AC,
AC,
∴∠C=30°;
综上所述,△ABC顶角的度数为30°或150°或90°.
故答案为30°或150°或90°..

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目