题目内容
【题目】如图，在平面直角坐标系中，一次函数y=kx+b的图像分別交x轴、y轴于A、B两点．与反比例函数y=﹣ 
的图像交于C，D两点，DE⊥x轴于点E．已知DE=3，AE=6． 
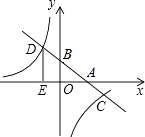
（1）求一次函数的解析式；
（2）直接写出不等式kx+b+ ＞0的解集．
【答案】
（1）解：∵点D在反比例函数y=﹣ 
的图像上，且DE=3，
∴将y=3代入反比例函数解析式得：3=﹣ ，即x=﹣2，
点D的坐标为（﹣2，3）．
又∵AE=6，
∴A点的坐标为（4，0）．
将A与D点的坐标代入一次函数解析式中得： 
，
解得：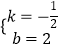 
．
∴一次函数解析式为y=﹣ 
x+2
（2）解：将y=﹣ x+2代入y=﹣ 中得：﹣ x+2=﹣ ，
解得：x1=﹣2，x2=6，
当x=6时，y=﹣ 
=﹣1，
即点C的坐标为（6，﹣1）．
kx+b+ ＞0可转化为kx+b＞﹣ ，
根据两个函数y=﹣ x+2与y=﹣ 的图像可知：
不等式的解集为：x＜﹣2或0＜x＜6
【解析】（1）根据点D在反比例函数上，且DE=3可得出点D的坐标，再由AE=6可得出点A的坐标，由待定系数法即可求出直线AD的函数解析式；（2）将一次函数解析式代入反比例函数中得处关于x的分式方程，解方程即可得出交点C的坐标，将原不等式进行变形，再结合一次函数与反比例函数图像可直接得出不等式的解集．
练习册系列答案
相关题目
