题目内容
【题目】点O在直线MN上,把两个一样的三角尺按图12所示放置,OD,OE分别平分∠CON和∠AOM.
(1)若∠EOM=10°,求∠NOD的度数;
(2)求∠EOD的度数;
(3)如果保持两个三角尺拼成的图形不变,绕点O转动两个三角尺,使∠CON逐渐变小,那么(2)中的结论会改变吗?
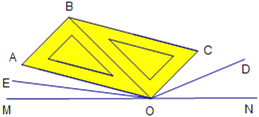
【答案】(1)∠NOD=20°;(2)∠EOD=150°;(3)不改变
【解析】
(1)由图可知,∠AOM=2∠EOM,∠BOA=30°,∠BOC=90°,∠CON=2∠NOD,据此可解答;
(2)由图可知,∠EOD=∠AOC+∠AOE+∠COD;
(3) ∠EOD=∠AOC+∠AOE+∠COD,其中∠AOC的大小不变,而∠AOE+∠COD=
![]() (∠AOM+∠CON)也是不变,据此可解答.
(∠AOM+∠CON)也是不变,据此可解答.
解:(1)因为OE平分∠AOM,∠EOM=10°,所以∠AOM=2∠EOM=20°.
因为∠AOC=120°,所以∠COM=140°.
所以∠CON=180°-∠COM=180°-140°=40°.
因为OD平分∠CON,所以∠NOD=![]() ∠CON=20°.
∠CON=20°.
(2)因为∠AOC=120°,所以∠AOM+∠CON=180°-∠AOC=60°.
因为OD,OE分别平分∠CON和∠AOM,所以∠AOE+∠COD=![]() (∠AOM+∠CON)=30°.
(∠AOM+∠CON)=30°.
所以∠EOD=∠AOC+∠AOE+∠COD=120°+30°=150°.
(3)不改变.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
【题目】“十一”黄金周期间,某市风景区在![]() 天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数):
天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数):
日期 |
|
|
|
|
|
|
|
人数变化(单位:万人) |
|
|
|
|
|
|
|
已知![]() 月
月![]() 日的游客人数为
日的游客人数为![]() 万人,请回答下列问题:
万人,请回答下列问题:
![]() 七天内游客人数最多的是哪天,最少的是哪天?它们相差多少万人?
七天内游客人数最多的是哪天,最少的是哪天?它们相差多少万人?
![]() 求这
求这![]() 天的游客总人数是多少万人.
天的游客总人数是多少万人.