题目内容
【题目】已知如图,在平面直角坐标系中,A(-1,-3),OB=![]() ,OB与x轴所夹锐角是45°
,OB与x轴所夹锐角是45°
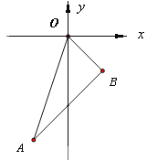
(1)求B点坐标
(2)判断三角形ABO的形状
(3)求三角形ABO的AO边上的高.
【答案】(1)B(1,-1);(2)证明见解析;(3)![]() .
.
【解析】
试题分析:(1)根据题中给出的条件在平面直角坐标系中,A(-1,-3),OB=![]() ,OB与x轴所夹锐角是45°那么由点B作x轴的垂线交x轴与点C,那么就可以知道三角形OBC为等腰直角三角形,根据勾股定理可以求出BC=OC的长度,即可求得点B坐标;(2)根据地(1)中求出点B的坐标之后可以求出线段OB,AB,的长度,那么运用勾股定理逆定理可以判断出三角形ABO为直角三角形;(3)第三问求高度问题那么就需要求出三角形ABO的面积,那么根据面积就可以求得AO边上的高.
,OB与x轴所夹锐角是45°那么由点B作x轴的垂线交x轴与点C,那么就可以知道三角形OBC为等腰直角三角形,根据勾股定理可以求出BC=OC的长度,即可求得点B坐标;(2)根据地(1)中求出点B的坐标之后可以求出线段OB,AB,的长度,那么运用勾股定理逆定理可以判断出三角形ABO为直角三角形;(3)第三问求高度问题那么就需要求出三角形ABO的面积,那么根据面积就可以求得AO边上的高.
试题解析:解(1)过点B作x轴的垂线交x轴与点C,如图所示:
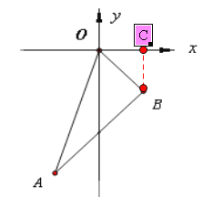
那么根据已知条件![]() ,所以在
,所以在![]() 中根据勾股定理可知
中根据勾股定理可知![]()
因为点B在第四象限,所以点B坐标为(1,-1)
(2)根据上面求得点B的坐标可知OA=![]() ,AB=
,AB=![]()
那么就有![]() 所以三角形ABO为直角三角形;
所以三角形ABO为直角三角形;
(3)因为三角形ABO为直角三角形,所以
![]() , h=
, h=![]()

练习册系列答案
相关题目