题目内容
【题目】如图,已知AB是⊙O的直径,C是⊙O上一点,∠BAC的平分线交⊙O于点D,交⊙O的切线BE于点E,过点D作DF⊥AC,交AC的延长线于点F. 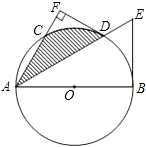
(1)求证:DF是⊙O的切线;
(2)若DF=3,DE=2 ①求 ![]() 值;
值;
②求图中阴影部分的面积.
【答案】
(1)证明:连接OD
∵OA=OD,∴∠1=∠2
∵∠1=∠3,∴∠2=∠3
∴OD∥AF
∵DF⊥AF,∴OD⊥DF
∴DF是⊙O的切线
(2)证明:①解:连接BD
∵直径AB
∴∠ADB=90°
∵圆O与BE相切
∴∠ABE=90°
∵∠DAB+∠DBA=∠DBA+∠DBE=90°
∴∠DAB=∠DBE
∴∠DAB=∠FAD
∵∠AFD=∠BDE=90°
∴△BDE∽△AFD
∴ ![]()
②连接OC,交AD于G
由①,设BE=2x,则AD=3x
∵△BDE∽△ABE∴ ![]()
∴ ![]()
解得:x1=2, ![]() (不合题意,舍去)
(不合题意,舍去)
∴AD=3x=6,BE=2x=4,AE=AD+DE=8
∴AB= ![]() ,∠1=30°
,∠1=30°
∴∠2=∠3=∠1=30°,∴∠COD=2∠3=60°
∴∠OGD=90°=∠AGC,∴AG=DG
∴△ACG≌△DOG,∴S△AGC=S△DGO
∴S阴影=S扇形COD= ![]()
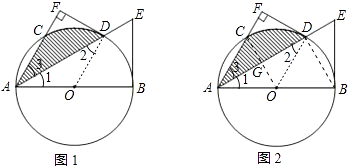
【解析】(1)作辅助线,连接OD.根据切线的判定定理,只需证DF⊥OD即可;(2)①连接BD.根据BE、DF两切线的性质证明△BDE∽△ABE;又由角平分线的性质、等腰三角形的两个底角相等求得△ABE∽△AFD,所以△BDE∽△AFD;最后由相似三角形的对应边成比例求得 ![]() ;②连接OC,交AD于G.由①,设BE=2x,则AD=3x.利用①中的△BDE∽△ABE的对应边成比例的性质求得
;②连接OC,交AD于G.由①,设BE=2x,则AD=3x.利用①中的△BDE∽△ABE的对应边成比例的性质求得 ![]() ,据此列出关于x的方程,解方程求得x=2,继而可以求出AD=3x=6,BE=2x=4,AE=AD+DE=8;然后由勾股定理知AB=4
,据此列出关于x的方程,解方程求得x=2,继而可以求出AD=3x=6,BE=2x=4,AE=AD+DE=8;然后由勾股定理知AB=4 ![]() ,在直角三角形ABE中求得∠1=30°;再由三角形的角平分线的性质、等腰三角形的性质及边角关系求得AG=DG,所以△ACG≌△DOG;最后根据两个全等三角形的面积相等的性质求扇形的面积即可.
,在直角三角形ABE中求得∠1=30°;再由三角形的角平分线的性质、等腰三角形的性质及边角关系求得AG=DG,所以△ACG≌△DOG;最后根据两个全等三角形的面积相等的性质求扇形的面积即可.
【考点精析】本题主要考查了勾股定理的概念和扇形面积计算公式的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2)才能正确解答此题.

【题目】“十一”黄金周期间,某市风景区在![]() 天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数):
天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数):
日期 |
|
|
|
|
|
|
|
人数变化(单位:万人) |
|
|
|
|
|
|
|
已知![]() 月
月![]() 日的游客人数为
日的游客人数为![]() 万人,请回答下列问题:
万人,请回答下列问题:
![]() 七天内游客人数最多的是哪天,最少的是哪天?它们相差多少万人?
七天内游客人数最多的是哪天,最少的是哪天?它们相差多少万人?
![]() 求这
求这![]() 天的游客总人数是多少万人.
天的游客总人数是多少万人.