题目内容
【题目】如图,菱形ABCD中,E是对角线AC上一点. 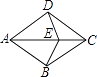
(1)求证:△ABE≌△ADE;
(2)若AB=AE,∠BAE=36°,求∠CDE的度数.
【答案】
(1)证明:∵四边形ABCD是菱形,
∴AB=AD,∠CAB=∠CAD,
在△ABE和△ADE中,
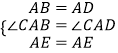 ,
,
∴△ABE≌△ADE(SAS)
(2)解:∵AB=AE,∠BAE=36°,
∴∠AEB=∠ABE= ![]() ,
,
∵△ABE≌△ADE,
∴∠AED=∠AEB=72°,
∵四边形ABCD是菱形,
∴AB∥CD,
∴∠DCA=∠BAE=36°,
∴∠CDE=∠AED﹣∠DCA=72°﹣36°=36°.
【解析】(1)由菱形的性质可得到AD=AB,∠CAB=∠CAD,结合公共边可证得结论;(2)由等腰三角形的性质可求得∠AEB=∠ABE,再结合(1)的结论,可求得∠AED,结合菱形的性质可求出∠CDE的大小.
【考点精析】解答此题的关键在于理解菱形的性质的相关知识,掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
【题目】“十一”黄金周期间,某市风景区在![]() 天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数):
天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数):
日期 |
|
|
|
|
|
|
|
人数变化(单位:万人) |
|
|
|
|
|
|
|
已知![]() 月
月![]() 日的游客人数为
日的游客人数为![]() 万人,请回答下列问题:
万人,请回答下列问题:
![]() 七天内游客人数最多的是哪天,最少的是哪天?它们相差多少万人?
七天内游客人数最多的是哪天,最少的是哪天?它们相差多少万人?
![]() 求这
求这![]() 天的游客总人数是多少万人.
天的游客总人数是多少万人.