题目内容
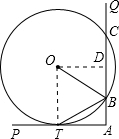
如图，∠PAQ是直角，⊙O与AP相切于点T，与AQ交于B、C两点．
（1）BT是否平分∠OBA，说明你的理由；
（2）若已知AT=4，弦BC=6，试求⊙O的半径R．
（1）BT是否平分∠OBA，说明你的理由；
（2）若已知AT=4，弦BC=6，试求⊙O的半径R．
（1）BT平分∠OBA，理由为：
证明：连接OT，如图所示，
∵AP与圆O相切，
∴OT⊥AP，
∴∠OTP=90°，
又∠QAP=90°，
∴∠OTP=∠QAP，
∴OT∥QA，
∴∠OTB=∠ABT，
又∵OB=OT，
∴∠OBT=∠OTB，
∴∠OBT=∠ABT，
则BT平分∠OBA；
（2）过O作OD⊥BC，又BC=6，
可得D为BC的中点，即BD=CD=3，
∵四边形ODAT为矩形，
∴OD=AT=4，
在Rt△OBD中，BD=3，OD=4，
根据勾股定理得：OB=
=5，
则圆的半径为5．
证明：连接OT，如图所示，
∵AP与圆O相切，
∴OT⊥AP，
∴∠OTP=90°，
又∠QAP=90°，
∴∠OTP=∠QAP，
∴OT∥QA，
∴∠OTB=∠ABT，
又∵OB=OT，
∴∠OBT=∠OTB，
∴∠OBT=∠ABT，
则BT平分∠OBA；
（2）过O作OD⊥BC，又BC=6，
可得D为BC的中点，即BD=CD=3，
∵四边形ODAT为矩形，
∴OD=AT=4，
在Rt△OBD中，BD=3，OD=4，
根据勾股定理得：OB=
| BD2+OD2 |
则圆的半径为5．
练习册系列答案
名校作业本系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
线交OA的延长线于点C，延长交⊙O于K，连接KO，OD．
