题目内容
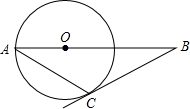
如图，MN切⊙O于A点，AC为弦，BC为直径，∠CAN=65°，则∠BMA的度数为______．
连接OA，
∵BC是⊙O直径，
∴∠BAC=90°，
∵∠CAN=65°，
∴∠BAM=180°-90°-65°=25°，
∵MN是⊙O切线，
∴∠OAN=90°，
∴∠OAC=90°-65°=25°，
∴∠OAB=90°-25°=65°，
∵OA=OB，
∴∠OBA=∠OAB=65°，
∴∠BMA=∠OBA-∠BAM=65°-25°=40°，
故答案为：40°．
∵BC是⊙O直径，
∴∠BAC=90°，
∵∠CAN=65°，
∴∠BAM=180°-90°-65°=25°，
∵MN是⊙O切线，
∴∠OAN=90°，
∴∠OAC=90°-65°=25°，
∴∠OAB=90°-25°=65°，
∵OA=OB，
∴∠OBA=∠OAB=65°，
∴∠BMA=∠OBA-∠BAM=65°-25°=40°，
故答案为：40°．
练习册系列答案
相关题目
延长线于点D．