题目内容
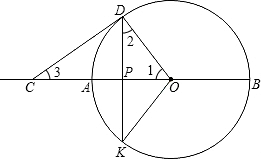
如图，P是⊙O的半径OA上的一点，D在⊙O上，且PD=PO．过点D作⊙O的切
线交OA的延长线于点C，延长交⊙O于K，连接KO，OD．
（1）证明：PC=PD；
（2）若该圆半径为5，CD∥KO，请求出OC的长．
线交OA的延长线于点C，延长交⊙O于K，连接KO，OD．（1）证明：PC=PD；
（2）若该圆半径为5，CD∥KO，请求出OC的长．
（1）证明：如图，∵PD=PO，
∴∠1=∠2；
∵CD是⊙O的切线，
∴CD⊥OD．（2分）
∴∠3+∠1=90°；
又∵∠CDP+∠2=90°，
∴∠3=∠CDP．（3分）
∴PC=PD．（4分）
（2）∵CD∥KO，有∠3=∠POK，
由（1）得，CP=PD=PO，又∠CPD=∠KPO，
∴△CPD≌△OPK
∴CD=OK=5；
在Rt△COD中，OC=
=5
．（8分）
∴∠1=∠2；
∵CD是⊙O的切线，
∴CD⊥OD．（2分）
∴∠3+∠1=90°；
又∵∠CDP+∠2=90°，
∴∠3=∠CDP．（3分）
∴PC=PD．（4分）
（2）∵CD∥KO，有∠3=∠POK，
由（1）得，CP=PD=PO，又∠CPD=∠KPO，
∴△CPD≌△OPK
∴CD=OK=5；
在Rt△COD中，OC=
| CD2+OD2 |
| 2 |
练习册系列答案
名校课堂系列答案
相关题目
