Question

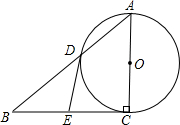
已知：如图，在Rt△ABC中，∠C=90°，∠BAC的角平分线AD交BC边于D．
（1）以AB边上一点O为圆心，过A、D两点作⊙O（不写作法，保留作图痕迹），再判断直线BC与⊙O的位置关系，并说明理由；
（2）若（1）中的⊙O与AB边的另一个交点为E，AB=6，BD=2

3

，求线段BD、BE与劣弧DE所围成的图形面积．（结果保留根号和π）

Answer 1

（1）如图：连接OD，
∵OA=OD，
∴∠OAD=∠ADO，
∵∠BAC的角平分线AD交BC边于D，
∴∠CAD=∠OAD，
∴∠CAD=∠ADO，
∴AC∥OD，
∵∠C=90°，
∴∠ODB=90°，
∴OD⊥BC，
即直线BC与⊙O的切线，
∴直线BC与⊙O的位置关系为相切；

（2）设⊙O的半径为r，则OB=6-r，又BD=2

3

，
在Rt△OBD中，
OD²+BD²=OB²，
即r²+（2

3

）²=（6-r）²，
解得r=2，OB=6-r=4，
∴∠DOB=60°，
∴S_扇形ODE=

60×π×22

360

=

2

3

π，
S_△ODB=

1

2

OD•BD=

1

2

×2×2

3

=2

3

，
∴线段BD、BE与劣弧DE所围成的图形面积为：S_△ODB-S_扇形ODE=2

3

-

2

3

π．